在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.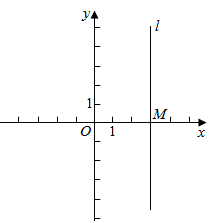
(1)如果△ABC三个顶点的坐标分别是A(-2,0)、B(-1,0)、C(-1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是点P1,点P1是关于直线l的对称点是点P2,求P P2的长.
先化简,再求值: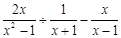 ,其中
,其中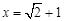 .
.
(1)计算: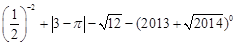 ;
;
(2)解方程: .
.
某工厂现有甲种原料360kg,乙种原料290kg,计划用它们生产A、B两种产品共50件,已知每生产一件A种产品,需要甲种原料9kg、乙种原料3kg,获利700元,生产一件B种产品,需要甲种原料4kg、乙种原料10kg,可获利1200元.
(1)利用这些原料,生产A、B两种产品,有哪几种不同的方案?
(2)设生产两种产品总利润为y(元),其中生产A中产品x(件),试写出y与x之间的函数解析式.
(3)利用函数性质说明,采用(1)中哪种生产方案所获总利润最大?最大利润是多少?
已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.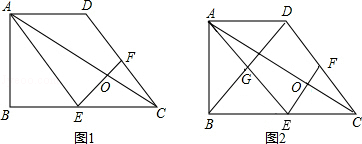
求证:(1)点F是DC上一点,连接EF,交AC于点O(如图1),△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元,商场平均每天盈利最多?