如图甲所示，是建筑工地将桩料打入泥土中以加固地基的打夯机示意图。打夯前先将桩料扶正立于地基之上。已知夯锤的质量为M=450kg，桩料的质量为m=50kg。每次打夯都通过卷扬机牵引将夯锤提升到距离桩顶h0=5m处再释放，让夯锤自由下落，夯锤砸在桩料上并不弹起，而是随桩料一起向下运动。
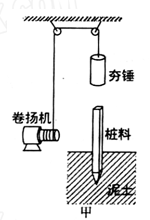
【两者碰撞时间极短，碰撞前后速度关系满足Mv0=(M+m）v】。桩料进入泥土后所受阻力，随打入深度h的变化关系如图乙所示，直线斜率k=5.05×104N／m。每次电动机需用20s的时间提升夯锤。提升夯锤时忽略加速和减速的过程，不计夯锤提升时的动能。g=10m／s2，求
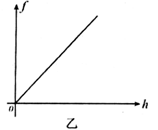
（1）若卷扬机的工作效率为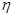
=80％，则在每次提升夯锤的过程中，卷扬机的输入功率。(结果保留2位有效数字）
（2）打完第一夯后，桩料进入泥土的深度。(假设打第一夯前，桩料未进入泥土）
如图所示，一质量为M＝4 kg，长为L＝2 m的木板放在水平地面上，已知木板与地面间的动摩擦因数为0.1，在此木板的右端上还有一质量为m＝1 kg的铁块，小铁块可视为质点，木板厚度不计．今对木板突然施加一个水平向右的拉力． (g＝10 m/
)
(1)若不计铁块与木板间的摩擦，且拉力大小为6 N，则小铁块经多长时间将离开木板？
(2)若铁块与木板间的动摩擦因数为0.2，铁块与地面间的动摩擦因数为0.1，要使小铁块相对木板滑动且对地面的总位移不超过1.5 m，则施加在木板水平向右的拉力应满足什么条件？
一个底面粗糙、质量为M的劈放在粗糙的水平面上，劈的斜面光滑且与水平面夹角为30°，用一端固定的轻绳系一质量为m的小球，小球放在斜面上，轻绳与斜面的夹角为30°，如图所示.若地面对劈的最大静摩擦力等于地面对劈的支持力的k倍，为使整个系统静止，k的最小值为多少？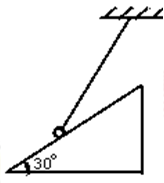
在水平地面上有一个质量为4kg的物体，物体在水平拉力F的作用下由静止开始运动。10s末拉力减为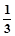
F该物体的v-t，图象如图所示。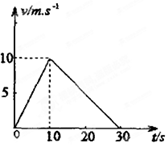
求：(1)物体受到的水平拉力F的大小
(2)物体与地面间的动摩擦因数。(g=10m/s2)
如图所示，水平面上放置一个倾角θ=37°的斜面体，现把一个质量m=10kg的物体放在该斜面体上，当用沿斜面向上大小为40N的拉力F作用于物体上时，物体刚好沿斜面匀速下滑而斜面体保持静止。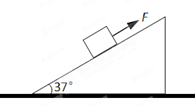
求：⑴出物体与斜面之间的动摩擦因数μ；
⑵若要使物体能沿斜面匀速上滑，拉力F应变为多大？（斜面体仍保持静止）（g取10m/s2，sin37°=0.6，cos37°=0.8）
一列长100 m的列车以v1＝20 m/s的正常速度行驶，当通过1000 m长的大桥时，必须以v2＝10 m/s的速度行驶．在列车上桥前需提前减速，当列车头刚上桥时速度恰好为10 m/s；列车全部离开大桥时又需通过加速恢复原来的速度．减速过程中，加速度大小为0.25 m/s2.加速过程中，加速度大小为1 m/s2，则该列车从减速开始算起，到过桥后速度达到20 m/s，共用了多长时间？