我校为进行“阳光运动一小时”活动,计划在一块直角三角形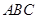 的空地上修建一个占地面积为
的空地上修建一个占地面积为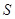 (平方米)的矩形
(平方米)的矩形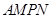 健身场地.如图,点
健身场地.如图,点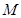 在
在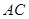 上,点
上,点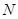 在
在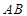 上,且
上,且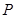 点在斜边
点在斜边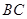 上.已知
上.已知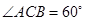 ,
,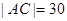 米,
米,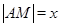 米,
米, .设矩形
.设矩形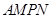 健身场地每平方米的造价为
健身场地每平方米的造价为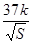 元,再把矩形
元,再把矩形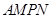 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为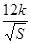 元(
元(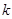 为正常数).
为正常数).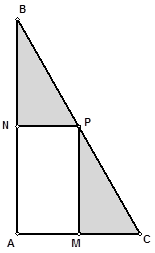
(1)试用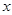 表示
表示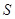 ,并求
,并求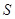 的取值范围;
的取值范围;
(2)求总造价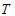 关于面积
关于面积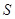 的函数
的函数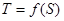 ;
;
(3)如何选取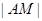 ,使总造价
,使总造价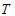 最低(不要求求出最低造价).
最低(不要求求出最低造价).
(本小题满 分12分)
分12分)
已知函数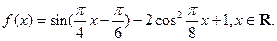
(1)求函 数
数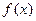 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)若关于x的方程 内有实数解,求实数m的取值范围。
内有实数解,求实数m的取值范围。
(本小题满分14分)
设数列 ,
, 满足:a1=4,a2=
满足:a1=4,a2= ,
, ,
,  .
.
(1)用 表示
表示 ;并证明:
;并证明: , an>2 ;
, an>2 ;
(2)证明: 是等比数列;
是等比数列;
(3)设Sn是数列 的前n项和,当n≥2时,Sn与
的前n项和,当n≥2时,Sn与 是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
(本小题满分12分)
已知函数 .
.
(1)确定 在(0,
在(0, +∞)上的单调性;
+∞)上的单调性;
(2)设 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围.
(本小题满分12分)
已知半圆 (y≥0),动圆与此半圆相切且与x轴相切.
(y≥0),动圆与此半圆相切且与x轴相切.
(1)求动圆圆心的轨迹,并画出其轨迹图形;
(2)是否存在斜率为 的直线l,它与(1)中所得轨迹的曲线由左到右顺次交于A,B,C,D四点,
的直线l,它与(1)中所得轨迹的曲线由左到右顺次交于A,B,C,D四点,
且满足|AD|=2|BC| .若存在,求出l的方程;若不存在,说明理由.
(本小题满分12分)
在△ABC中,∠ACB=90°, ∠BAC=30°,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将△ADE折起,使得平面ADE⊥ 平面BDEC(图二),
(1)若F是AB的中点,求证: CF∥平面ADE;
CF∥平面ADE;
(2)P是AC上任意一点,求证:平面ACD⊥ 平面PBE ;
;
(3)P是AC上一点,且AC⊥ 平面PBE,求二面角P—BE—C的大小.