设三个底面半径都为1的圆柱侧面两两相切,且它们的轴两两互相垂直,则与这三个圆柱侧面都相切的球的半径最小值等于( )
A.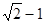 |
B.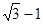 |
C. |
D.1 |
O为坐标原点,F为抛物线C:y2=4 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4 ,则△POF的面积为( )
,则△POF的面积为( )
| A.2 | B.2 |
C.2 |
D.4 |
下列命题中是假命题的是( )
| A.∃α,β∈R,使sin(α+β)=sinα+sinβ |
B.∀ ∈R,函数f(x)=sin(2x+ ∈R,函数f(x)=sin(2x+ )都不是偶函数 )都不是偶函数 |
C.∃m∈R,使f(x)=(m-1)· 是幂函数,且在(0,+∞)上单调递减 是幂函数,且在(0,+∞)上单调递减 |
| D.∀a>0,函数f(x)=ln2x+lnx-a有零点 |
已知命题p:若a>1,则ax>logax恒成立;命题q:等差数列{an}中,m+n=p+q是an+am=ap+aq的充分不必要条件(其中m,n,p,q∈N*).则下面选项中真命题是( )
A.( p)∧( p)∧( q) q) |
B.( p)∨( p)∨( q) q) |
C.( p)∧q p)∧q |
D.p∧q |
使命题“对任意的x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是( )
| A.a≥4 | B.a≤4 |
| C.a≥5 | D.a≤5 |
对于命题p:∀x∈[0,+∞),(log32)x≤1,( )
A.是假命题,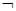 p:∃x0∈[0,+∞), p:∃x0∈[0,+∞),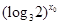 >1 >1 |
B.是假命题, p:∀x∈[0,+∞),(log32)x≥1 p:∀x∈[0,+∞),(log32)x≥1 |
C.是真命题, p:∃x0∈[0,+∞), p:∃x0∈[0,+∞), 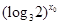 >1 >1 |
D.是真命题, p:∀x∈[0,+∞),(log32)x≥1 p:∀x∈[0,+∞),(log32)x≥1 |