设已知函数
，
．
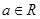（1）当
时，求函数
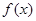的最大值的表达式
．
（2）是否存在实数
，使得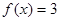
有且仅有3个不等实根，且它们成等差数列，若存在，求出所有的值，若不存在，说明理由．
如图，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=
，BC=
1，PA=2，E为PD的中点.
（1）求直线AC与PB所
成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点
到AB和AP的距离.
已知向量
，若正数k和t使得向量
垂直，求k的最小值.
已知点G是△ABC的重心，A(0, －1)，B(0, 1)，在x轴上有一点M，满足|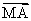
|=|
|，
(
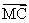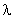∈R)．
⑴求点C的轨迹方程；
⑵若斜率为k的直线l与点C的轨迹交于不同两点P，Q，且满足|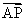
|=|
|，试求k的取值范围．
在
中，O为中线AM上一个动点，若AM=2，则
的最小值是_____.
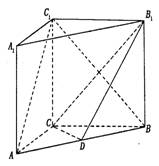
如图, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AA1＝4，点D是AB的中点，（I）求证：（I）AC⊥BC1；
（II）求证：AC 1//平面CDB1；