两平行金属板间所加电压随时间变化的规律如图所示，大量质量为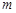
、带电量为
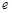的电子由静止开始经电压为
的电场加速后连续不断地沿两平行金属板间的中线射入，若两板间距恰能使所有电子都能通过，且两极长度使每个电子通过两板均历时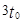
，电子所受重力不计，试求：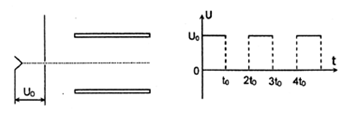
（1）电子通过两板时侧向位移的最大值和最小值。
（2）侧向位移最大和最小的电子通过两板后的动能之比。
如图为回旋加速器的装置图，D型盒的两底边分别为a、b，且相距很近，忽略粒子在其间的运动时间，设D型盒中的匀强磁场的磁感应强度为B，D型盒的半径为R，质量为m带电量为q的正电荷在a的中点从静止释放，求：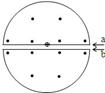
（1）带电粒子出回旋加速器时的动能
（2）从带电粒子开始运动开始计时，画出Uab一个周期内随时间t变化的图像（横轴用已知量标出）
（3）如果ab间的电压值始终保持为U，带电粒子从静止开始运动到出加速器所用的时间
带电量为Q，质量为m的原子核由静止开始经电压为U1的电场加速后进入一个平行板电容器，进入时速度和电容器中的场强方向垂直。已知：电容器的极板长为L，极板间距为d，两极板的电压为U2，重力不计，求：
（1）经过加速电场后的速度；
（2）离开电容器电场时的侧移量和偏转角的正切值。
质谱仪的工作原理图如图所示,A为粒子加速器,加速电压为U1;M为速度选择器,两板间有相互垂直的匀强磁场和匀强电场,匀强磁场的磁感应强度为B1,两板间距离为d;N为偏转分离器,内部有与纸面垂直的匀强磁场,磁感应强度为B2.一质量为m,电荷量为q的带正电的粒子由静止经加速器加速后,恰能通过速度选择器,进入分离器后做圆周运动,并打到感光板P上.不计重力,求: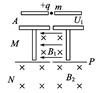
(1)粒子经粒子加速器A加速后的速度v的大小及速度选择器M两板间的电压U2.
(2)粒子在偏转分离器N的磁场中做圆周运动的半径R.
(3)某同学提出在其他条件不变的情况下,只减小加速电压U1,就可以使粒子在偏转分离器N的磁场中做圆周运动的半径减小.试分析他的说法是否正确.
如图所示，虚线左侧有一场强为E1=E的匀强电场，在两条平行的虚线MN和PQ之间存在着宽为L、电场强度为E2=2E的匀强电场，在虚线PQ右侧相距也为L处有一与电场E2平行的屏．现将一电子（电荷量e,质量为m）无初速度放入电场E1中的A点，最后打在右侧的屏上，AO连线与屏垂直，垂足为O,求：
(1)电子从释放到打到屏上所用的时间；
(2)电子刚射出电场E2时的速度方向与AO连线夹角的正切值tanθ；
(3) 电子打到屏上的点P到O点的距离x.
如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°固定斜面底端，(斜面足够长)，对物体施以平行于斜面向上的拉力F，t1＝1s时撤去拉力，物体运动的部分v-t图像如图乙，试求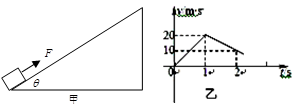
（1）物体与斜面间的滑动摩擦因数；
（2）拉力F大小；
（3）物体离开斜面时的速度大小。