一股民上周末以每股27元价格买了1000股股票，下表为本周内每日股票的涨跌情况（单位：元）：
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 涨跌（与前一交易日比较） |
+4 |
+4.5 |
-1 |
-2.5 |
-4 |
（1）星期四收盘时，每股多少元？
（2）本周内每股最高价，最低价分别是多少元？
（3）已知该股民买进股票时付了百分之零点一五的手续费，卖出时需付成交额百分之零点一五的手续费和百分之零点一的交易税，如果他一直观望到星期五才将股票全部卖出，请你算算他本周的收益如何．
（1）引入：如图1，直线AB为⊙O的弦，OC⊥OA,交AB于点P,且PC=BC，直线BC是否与⊙O相切，为什么？
（2）引申：记（1）中⊙O的切线为直线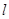
，在（1）的条件下，如图2，将切线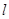向下平移，设平移后的直线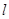与OB的延长线相交于点
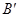，与AB的延长线相交于点E，与OP的延长线相交于点
．
找出图2中与
相等的线段，并说明理由；
如果
=9cm，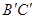
=12cm，⊙O的半径为6cm，试求线段
的长．
悦达汽车4S店“十一”黄金周销售某种型号汽车，该型号汽车的进价为30万元/辆，若黄金周期间销售量超过5辆时，每多售出1辆，所有售出的汽车进价均降低0．1万元/辆．根据市场调查，黄金周期间销售量不会突破30台．已知该型号汽车的销售价为32万元/辆，悦达汽车4S店计划黄金周期间销售利润25万元，那么需售出多少辆汽车？（注：销售利润=销售价﹣进价）
实践操作：
如图，在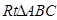
中，∠ABC=90°，利用直尺和圆规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）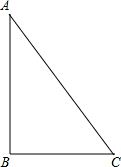
（1）作∠BCA的角平分线，交AB于点O；
（2）以O为圆心，OB为半径作圆．
综合运用：
在你所作的图中，
（1）AC与⊙O的位置关系是（直接写出答案）
（2）若BC=6，AB=8,求⊙O的半径．
在等腰△ABC中，三边分别为a、b、c，其中a=5，若关于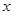
的方程x2+(b+2)x+6-b=0有两个相等的实数根，求△
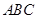的周长．
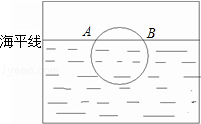
每位同学都能感受到日出时美丽的景色．下图是一位同学从照片上剪切下来的画面，“图上”太阳与海平线交于A﹑B两点，他测得“图上”圆的半径为5厘米，AB=8厘米，若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟，求“图上”太阳升起的速度．