当a>0时,设命题P:函数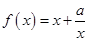 在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )
在区间(1,2)上单调递增;命题Q:不等式x2+ax+1>0对任意x∈R都成立.若“P且Q”是真命题,则实数a的取值范围是( )
| A.0<a≤1 | B.1≤a<2 | C.0≤a≤2 | D.0<a<1或a≥2 |
等轴双曲线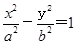 (a>0,b>0)的右焦点为F(c,0),方程
(a>0,b>0)的右焦点为F(c,0),方程 的实根分别为
的实根分别为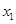 和
和 ,则三边长分别为|
,则三边长分别为|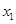 |,|
|,| |,2的三角形中,长度为2的边的对角是()
|,2的三角形中,长度为2的边的对角是()
| A.锐角 | B.直角 | C.钝角 | D.不能确定 |
在圆 内任取一点,则该点恰好在区域
内任取一点,则该点恰好在区域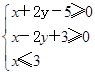 内的概率为()
内的概率为()
A.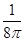 |
B. |
C.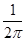 |
D.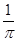 |
正方形AP1P2P3的边长为4,点B,C分别是边P1P2,P2P3的中点,沿AB,BC,CA折成一个三棱锥P-ABC(使P1,P2,P3重合于P),则三棱锥P-ABC的外接球表面积为()
| A.24π | B.12π | C.8π | D.4π |
如图所示,M,N是函数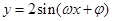 (ω>0)图像与x轴的交点,点P在M,N之间的图像上运动,当△MPN面积最大时
(ω>0)图像与x轴的交点,点P在M,N之间的图像上运动,当△MPN面积最大时 ,则ω=()
,则ω=()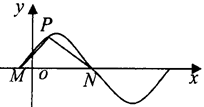
A. |
B. |
C. |
D.8 |
已知等比数列{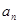 }中,各项都是正数,且
}中,各项都是正数,且 成等差数列,则
成等差数列,则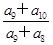 =()
=()
A.1- |
B.1+ |
C.3-2 |
D.3+2 |