如图,在Rt△ABC中,∠ACB=90°,过C直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.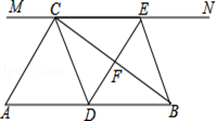
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
甲、乙两个不透明布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2,;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
已知 中,AB=AC=BC=3.请在图中用尺规作图画出
中,AB=AC=BC=3.请在图中用尺规作图画出 的内切圆,保留作图痕迹,并求出内切圆的半径。
的内切圆,保留作图痕迹,并求出内切圆的半径。
已知,△ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是射线CA上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.
(1)如图①,若E在边AC上.试说明:①AE=CF;②CG=GD;
(2)如图②,若E在边CA的延长线上.(1)中的两个结论是否仍成立?(直接写出成立结论的序号,不要说明理由)
(3)若AE=3,CH=5,求边AC的长.
某市出租车的收费标准为:不超过3km的计费为7.0元,3km后按2.4元/km计费.
(1)当行驶路程x超过3km时,写出车费y(元)与行驶路程x(km)之间的函数关系式;
(2)若小明乘出租车的行驶路程为5km,则小明应付车费多少元?
(3)若小亮乘出租车出行,付费19元,则小亮乘车的路程为多少km?
如图,已知Rt△ABC中,∠C=90°.沿DE折叠,使点A与点B重合,折痕为DE.
(1)若DE=CE,求∠A的度数;
(2)若BC=6,AC=8,求CE的长.