某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量 (本 与每本纪念册的售价 (元 之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出 与 的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为 元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
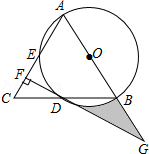
如图,在 中, ,以 为直径的 分别交线段 , 于点 , ,过点 作 ,垂足为 ,线段 , 的延长线相交于点 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.
在一次课外实践活动中,同学们要测量某公园人工湖两侧 , 两个凉亭之间的距离.如图,现测得 , , 米,请计算 , 两个凉亭之间的距离(结果精确到1米)(参考数据: ,

在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中, 的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.