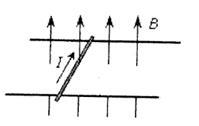
如图所示,在同一水平面的两导轨相互平行,相距2m并处于竖直向上的磁感应强度B为0.75T的匀强磁场中,一根质量为3.0kg的金属杆放在导轨上且与导轨垂直,当金属棒中通如图所示的电流为5A时,金属棒恰好做匀速直线运动,求:( )
)
(1)导轨与金属棒间的动摩擦因数;
(2)保持气体条件不变,通入金属棒中电流变为9A瞬间,金属棒加速度的大小;
(3)保持气体条件不变,将两导轨的右端抬高,使其与水平方向夹角为45°,若要仍使金属棒保持静止且与导轨间无摩擦力,金属棒中的电流。
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β。我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出)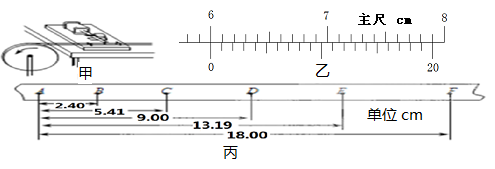
①如图甲所示,将打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔,然后固定在圆盘的侧面,当圆盘转动时,纸带可以卷在圆盘侧面上;
②接通电源,打点计时器开始打点,启动控制装置使圆盘匀加速转动;
③经过一段时间,圆盘停止转动和打点,取下纸带,进行测量。
(1)用20分度的游标卡尺测得圆盘的直径如图乙所示,圆盘的直径d为______cm;
(2)由图丙可知,打下计数点D时,圆盘转动的角速度为______rad/s (计算结果保留3位有效数字)
(3)圆盘转动的角加速度大小为______rad/s2。(计算结果保留3位有效数字)
如图所示,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,物体A被水平速度为v0的子弹击中,子弹嵌在其中,已知A的质量是B的质量的3/4,子弹的质量是B的质量的1/4。求: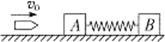
⑴A物体获得的最大速度;
⑵弹簧压缩量最大时B物体的速度。
如图所示,传送带的水平部分ab=4m,斜面部分bc=4m,bc与水平面的夹角α=37°.一个小物体A与传送带的动摩擦因数μ=0.25,传送带沿图示的方向运动,速率v=2 m/s.若把物体A轻放到a处,它将被传送带送到c点,且物体A不会脱离传送带.求物体A从a点被传送到c点所用的时间.(已知:sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,物体的质量为5kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,求拉力F的大小范围.
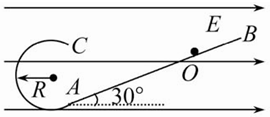
如图所示,绝缘光滑轨道AB部分为倾角为30°的斜面,AC部分为竖直平面上半径为R的圆轨道,斜面与圆轨道相切.整个装置处于场强为E、方向水平向右的匀强电场中.现有一个质量为m的小球,带正电荷量为q=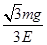 ,要使小球能安全通过圆轨道,在O点的初速度应满足什么条件?
,要使小球能安全通过圆轨道,在O点的初速度应满足什么条件?