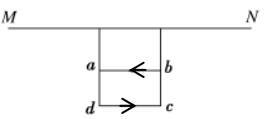
截流长直导线周围磁场的磁感应强度大小为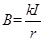 ,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为
,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为 。当MN通以强度为
。当MN通以强度为 的电流时,两细线内的张力均减小为
的电流时,两细线内的张力均减小为 ,当MN内的电流强度变为
,当MN内的电流强度变为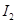 时,两细线的张力均大于
时,两细线的张力均大于
(1)分别指出强度为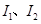 的电流和方向;
的电流和方向;
(2)MN分别通以强度为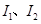 电流时,线框受到的安培力
电流时,线框受到的安培力 大小之比。
大小之比。
如图所示,宽为0.5m的光滑水平金属框架固定在方向竖直 向下、磁感应强度大小为B=0.80T的匀强磁场中,框架左端连接一个R=0.4Ω的电阻,框架上面置一电阻r=0.1Ω的金属导体ab,ab长为0.5m。ab始终与框架接触良好且在水平恒力F作用下以v=1.25m/s的速度向右匀速运动(设水平金属框架足够长.轨道电阻及接触电阻忽略不计)。
向下、磁感应强度大小为B=0.80T的匀强磁场中,框架左端连接一个R=0.4Ω的电阻,框架上面置一电阻r=0.1Ω的金属导体ab,ab长为0.5m。ab始终与框架接触良好且在水平恒力F作用下以v=1.25m/s的速度向右匀速运动(设水平金属框架足够长.轨道电阻及接触电阻忽略不计)。试判断金属导体ab两端哪端电势高;
求通过金属导体ab的电流大小:
求水平恒力F对金属导体ab做功的功率。

我国自行研制的“神舟”六号载人飞船,于2005年10月12日在酒泉发射场由长征二号F型火箭发射升空。并按预定轨道环绕地球飞行5天后,安全返回,在内蒙古的主着陆场着陆。设“神舟”六号飞船在飞行过程中绕地球沿圆轨道运行,已知地球半径为R,地球表面的重力加速度为g,时间t秒内飞船绕地球运行的圈数为N,求飞船离地面的平均高度h。
已知质量为m的飞船在太空中的引力势能可表示为:Ep=-
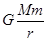 ,式中G为万有引力常量,M为地球的质量,r为飞船到地球中心的距离。那么将质量为m的飞船从地面发射到距离地面高度为h的圆形轨道上,长征二号F型火箭至少要对飞船做多少功?(不考虑地球自转对发射的影响)。
,式中G为万有引力常量,M为地球的质量,r为飞船到地球中心的距离。那么将质量为m的飞船从地面发射到距离地面高度为h的圆形轨道上,长征二号F型火箭至少要对飞船做多少功?(不考虑地球自转对发射的影响)。
如图所示,车厢A以速度V0=6.0m/s沿平直轨道匀速前进,在车厢内水平桌面上有一个小物块C随车厢A一起运动,已知水平桌面的高度h=0.80m,小物块与桌面间的动摩擦因数 ="0" .20。在车厢A的正前方轨道上放着车厢B,且A的总质量(不包括小物块)与车厢B的质量相等,两车厢碰撞挂接后连在一起,假设此后它们始终以共同的速度匀速前进(取g=10m/s2)
="0" .20。在车厢A的正前方轨道上放着车厢B,且A的总质量(不包括小物块)与车厢B的质量相等,两车厢碰撞挂接后连在一起,假设此后它们始终以共同的速度匀速前进(取g=10m/s2)
两车厢挂接后的共同速度v=?
两车厢挂接后,小物块C开始沿桌面向前滑动,最后落在车厢A的地板上,总共经历的时间t=1.0s,求小物块在水平桌面上滑行的距离s=?
如图所示,一个质量m=10-6kg,电量q=+2.0c的微粒,由静止开始出发,加速电压U加=105V,带电微粒垂直进入偏转电场中,板长l=20cm,两板间距离d=4cm,两板间偏转电压U偏=4×103V(不计重力),试求:
带电粒子离开偏转电场时侧移是多少?
全过程中电场力对带电粒子做功为多少?
若在偏转电场右侧距离为S="20cm" 处,放一竖直荧光屏,则带电粒子打在荧光屏上的位置距中心O的距离?
如图所示,A、B是竖直放置的平行板电容器,B板中央有一个小孔,恰好跟一个边界是等边三角形的一个匀强磁场的顶端相接,磁场方向垂直纸面向里,磁感应强度为B,其中 ,磁场的
,磁场的 边界平行于平行板A和B。
边界平行于平行板A和B。
若在A板上正对B板小孔的P处,静止释放一个带电量为
 、质量为
、质量为 的带电粒子(重力不计),恰能从图中O点射出,且
的带电粒子(重力不计),恰能从图中O点射出,且 ,则A、B两板间的电压
,则A、B两板间的电压 是多少?
是多少?若要上述带电粒子在磁场中的运动时间与平行板A、B间的电压无关,则A、B两板间的电压
 又是多少?
又是多少?