如图所示，水平地面上有一竖直绝缘弹性薄挡板，板高h=5m，与板等高处有一水平放置的小篮筐，筐口的中心距挡板s=1m。整个空间存在匀强磁场和匀强电场，磁场方向垂直纸面向里，磁感应强度B=0.2T，而匀强电场未在图中画出。质量
、电荷量
的带电小球（可视为质点），自挡板下端的左侧以不同的水平初速度
开始向左运动，恰能做匀速圆周运动，若小球与挡板相碰后以原速率弹回，且碰撞时间不计，碰撞前后电量不变，小球最后都能从筐口的中心处落入筐中（
）。试求：
（1）电场强度的大小和方向；
（2）小球运动的最大速率；
（3）小球运动的最长时间。（结果可用反三角函数表示，例如
，
）
带有等量异号电荷、相距10cm的平行板A和B之间有一个匀强电场,如图所示,电场强度E=2×104V/m,方向向下。电场中C点距B板3cm,D点距A板2cm.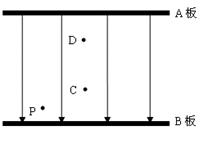
(1)如果令B板接地(即B板电势为零),则C点和D点的电势各是多少？
(2)C,D两点UCD等于多少？
(3)一个电子从C点移动到D点,静电力做多少功？ 如果使电子先移到P点,再移到D点,静电力做的功是否发生变化？（e=-1.6×10-19C）
两个可视为质点的金属小球A.B质量都是m、带负电，电荷量都是Q如有图所示，连接小球的绝缘细线长度都是L，静电力常量为k，重力加速度为g．则(1)连结A.B的细线中的张力为多大? (2)连结O、A的细线中的张力为多大?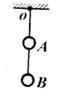
一物体做直线运动，某时刻开始计时的v-t图象如图。求：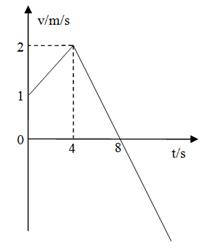
（1）运动过程中出现的加速度；
（2）开始计时后向正方向运动的最大位移xm；
（3）位移为1m所对应的时刻。
如图，箱子重力为G=220N，在与水平地面成θ=370角的F=100N的恒定拉力作用下匀速前进，求：
（1）地面对箱子的摩擦力f和支持力N大小；
（2）地面与箱子之间的动摩擦因素μ大小；
（3）若把拉力方向变为水平向右，要匀速拉动箱子，拉力又为多大？
滑块的重力为G=20N，当木板的倾角为α=370时，滑块恰能匀速下滑。求：
（1）匀速下滑时滑块受到的支持力N和摩擦力f大小；
（2）滑块与斜面间的动摩擦因素μ的值；
（3）用一沿斜面向上的力F可拉滑块匀速上滑，此F的大小。
（已知sin370≈0.6，cos370≈0.8）