在日常生活中，人们习惯于用几何相似性放大（或缩小）的倍数去得出推论，例如一个人身体高了50%，做衣服用的布料也要多50%，但实际上这种计算方法是错误的。若物体的几何线度为L，当L改变时，其它因素按怎样的规律变化？这类规律可称之为标度律，它们是由量纲关系决定的。在上例中，物体的表面积S=L，所以身高变为1.5倍，所用的布料变为1.52 = 2.25倍。以跳蚤为例：如果一只跳蚤的身长为2 mm，质量为0.2g，往上跳的高度可达0.3m。可假设其体内能用来跳高的能量
（L为几何线度），在其平均密度不变的情况下，身长变为2m，则这只跳蚤往上跳的最大高度最接近：（ ）
| A．0.3 m | B．3 m | C．30 m | D．300 m |
如图甲、乙所示的位移﹣时间（x﹣t）图象和速度﹣时间（v﹣t）中，给出了四条曲线1、2、3、4，代表四个不同物体的运动情况，则下列说法中错误的是（）
| A．图线1、3表示物体做曲线运动 |
| B．x﹣t图象中0～t1时间内物体1和2的平均速度相等 |
| C．v﹣t图象中t4时间内3的速度大于4的速度 |
| D．两图象中，t2、t5时刻分别表示2、4开始反向运动 |
将一物体沿与水平面α角的方向以速度v0抛出，重力加速度为g，如图所示．在其轨迹最高点P处附近的一小段曲线可近似为一段圆弧，则该圆弧所在的圆的半径是（）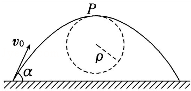
A． |
B． |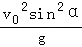
C． |
D． |
如图，A，B为两个并排放置在光滑水平面上的滑块，用水平力F1，F2分别推AB物体，已知F1=10N，F2=6N，A的质量大于B的质量，则AB之间的相互作用力F的大小满足（）
| A．6N＜F＜8N | B．6N＜F＜10N | C．8N＜F＜10N | D．F=8N |
一根长为L的细线上端固定，另一端连接一小球，现设法使小球在水平面内做匀速圆周运动，则小球运动的周期T与细线和竖直直线之间的夹角θ的关系是（）
| A．角θ越小，周期T越长 |
| B．角θ越小，周期T越短 |
| C．周期T的长短与角θ的大小无关 |
| D．条件不足，无法确定 |
如图，质量为M的楔形物块静置在水平地面上，其斜面的倾角为θ．斜面上有一质量为m的小物块，小物块与斜面之间存在摩擦．用恒力F沿斜面向上拉小物块，使之匀速上滑．在小物块运动的过程中，楔形物块始终保持静止．地面对楔形物块的支持力为（）
| A．（M+m）g | B．（M+m）g﹣F | C．（M+m）g+Fsinθ | D．（M+m）g﹣Fsinθ |