已知抛物线的顶点在原点,焦点在 轴正半轴上,抛物线上一点的横坐标为2,且该点到焦点的距离为2.
轴正半轴上,抛物线上一点的横坐标为2,且该点到焦点的距离为2.
(1)求抛物线的标准方程;
(2)与圆 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点 ,若抛物线上一点
,若抛物线上一点 满足
满足 ,求
,求 的取值范围。
的取值范围。

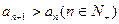

(1)求数列 的通项公式;
的通项公式;
(2)设 的前n项和为
的前n项和为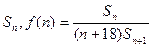 ,试问当n为何值时,
,试问当n为何值时,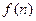 最大?并求出
最大?并求出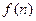 的最大值
的最大值
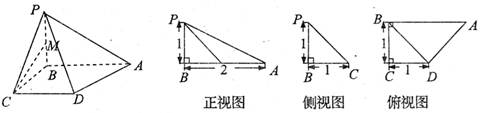
(1)设PB的中点为M,求证CM是否平行于平面PDA?
(2)在BC边上是否存在点Q,使得二面角A—PD—Q为120°?若存在,确定点Q的位置;若不存在,请说明理由
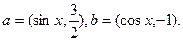
(1)当a//b时,求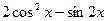 的值;
的值;
(2)求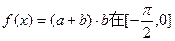 上的最大值
上的最大值
设 和
和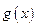 在
在 上的图象是连续不断的一条曲线,而且
上的图象是连续不断的一条曲线,而且 .证明:在
.证明:在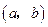 上至少存在一个
上至少存在一个 ,使
,使 .
.
某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台,现销售给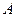 地10台,
地10台,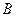 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至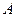 地,
地,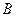 地的运费分别为400元和800元,从乙地调运1台至
地的运费分别为400元和800元,从乙地调运1台至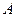 地,
地,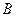 地的费用分别为300元和500元.
地的费用分别为300元和500元.
(1)设从乙地调运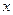 台至
台至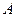 地,求总费用
地,求总费用 关于台数
关于台数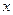 的函数解析式;
的函数解析式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的费用.