如图,已知 与圆
与圆 相切于点
相切于点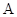 ,经过点
,经过点 的割线
的割线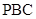 交圆
交圆 于点
于点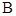 ,
,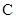 ,
,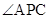 的平分线分别交
的平分线分别交 ,
,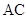 于点
于点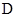 ,
,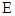 .
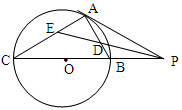
.
(1)证明: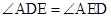 ;
;
(2)若 ,求
,求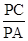 的值.
的值.
集合A={x|3≤x<10},B={x|2<x<7},C={x|x<a},
(Ⅰ)求A∪B;
(Ⅱ)求(CRA)∩B;
(Ⅲ)若A∩C≠ ,求a的取值范围.
,求a的取值范围.
已知函数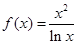 .
.
(1)求函数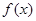 在区间
在区间 上的最值;
上的最值;
(2)若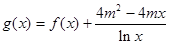 (其中
(其中 为常数),当
为常数),当 时,设函数
时,设函数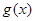 的3个极值点为
的3个极值点为 ,且
,且 ,证明:
,证明: .
.
已知椭圆 过点
过点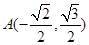 ,离心率为
,离心率为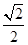 ,点
,点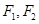 分别为其左右焦点.
分别为其左右焦点.
(1)求椭圆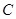 的标准方程;
的标准方程;
(2)若 上存在两个点
上存在两个点 ,椭圆上有两个点
,椭圆上有两个点 满足
满足 三点共线,
三点共线,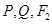 三点共线,且
三点共线,且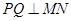 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,
, 为棱
为棱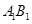 上的点.
上的点.
(1)证明: ;
;
(2)是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为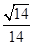 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
设数列 的前
的前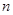 项和为
项和为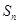 ,已知
,已知 ,且
,且 成等比数列,
成等比数列,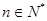 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设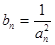 ,数列
,数列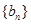 前
前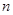 项和为
项和为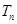 ,求证
,求证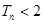 .
.