如图所示,李华晚上在路灯下散步.已知李华的身高AB=1.8米,灯柱的高OP=O'P'=18米,两灯柱之间的距离OO'=30米.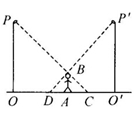
(1)若李华距灯柱OP的水平距离OA=18米,求他影子AC的长;
(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值?若为定值,求出该定值;若不是请说明理由.
如图,在□ABCD中,过点B作BE⊥CD于E,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30º,求AE的长;
(3)在(1)(2)的条件下,若AD=3,求BF的长.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠A.
(1)求∠D的度数;
(2)若CD=2,求BD的长.
已知关于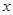 的一元二次方程
的一元二次方程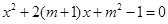 .
.
(1)若方程有实数根,求实数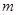 的取值范围;
的取值范围;
(2)若方程两实数根分别为 、
、 ,且满足
,且满足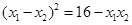 ,求实数
,求实数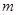 的值.
的值.
解方程:
(1)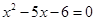
(2)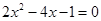
(3)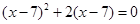
(4)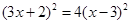
如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为1cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=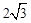 cm,AD=2cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s).
cm,AD=2cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s).
(1)如图①,连接OA、AC,则∠OAC的度数为°;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<1时,求t的取值范围(解答时可以利用备用图画出相关示意图).