如图所示，在平面直角坐标系xOy中，第Ⅰ象限内有沿y轴负向的匀强电场，电场强度的大小为E，第Ⅳ象限内有垂直纸面向外的匀强电场。在y轴上的P点沿x轴正向发射质量为m、电荷量为q的带正电粒子，粒子从x轴上Q点射入磁场。已知Q点坐标为（L，0），不计粒子的重力及相互作用。
（1）若粒子在Q点的速度方向与x轴成30°角，求P点的坐标及粒子在Q点的速度大小；
（2）若从y轴的正半轴上各点处均向x轴正向发射与（1）中相同的粒子，结果这些粒子均能从x轴上的Q点进入磁场，并且到Q点速度最小的粒子A，经磁场偏转后，恰好垂直y轴射出磁场，求匀强磁场的磁感应强度大小及粒子A在磁场中运动时间。
如图所示，N＝50匝的矩形线圈abcd，边长ab＝20 cm，ad＝25 cm，放在磁感应强度B＝0.4 T的匀强磁场中，外力使线圈绕垂直于磁感线且通过线圈中线的OO′轴以n＝3000 r/min的转速匀速转动，线圈电阻r＝1 Ω，外电路电阻R＝9 Ω，t＝0时，线圈平面与磁感线平行，ab边正转出纸外、cd边转入纸里．
(1)在图中标出t＝0时感应电流的方向；
(2)写出线圈感应电动势的瞬时表达式；
(3)从图示位置转过90°过程中流过电阻R的电荷量是多大？
如图所示，光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上，两导轨间距
，电阻
，导轨上静止放置一质量
、电阻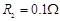
的金属杆，导轨电阻忽略不计，整个装置处在磁感应强度
的匀强磁场中，磁场的方向竖直向下，现用一外力
沿水平方向拉杆，使之由静止起做匀加速运动并开始计时，若5s末杆的速度为2.5m/s，求：
（1）5s末时电阻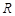
上消耗的电功率；
（2）5s末时外力的功率.
（3）若杆最终以8m/s的速度作匀速运动,此时闭合电键S,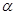
射线源Q释放的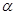粒子经加速电场C加速后从
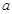孔对着圆心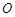
进入半径
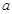的固定圆筒中（筒壁上的小孔只能容一个粒子通过），圆筒内有垂直水平面向下的磁感应强度为
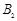的匀强磁场。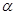粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失，粒子与圆筒壁碰撞5次后恰又从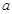孔背离圆心射出,忽略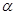粒子进入加速电场的初速度,若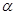粒子质量
,电量
,则磁感应强度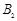多大？若不计碰撞时间,粒子在圆筒内运动的总时间多大？
如图所示，相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场，磁感应强度为B，正方形线圈abcd边长为L（L<d），电阻为R，将线圈在磁场上方h高处由静止释放，当cd边进入磁场时恰能做匀速直线运动，则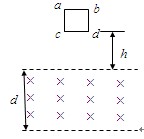
(1):线框的质量是多少？
（2）从CD边开始进入磁场到线框完全进入到磁场的过程中，线框中产生的热量是多少？
如图所示，在X轴上方有匀强磁场B，一个质量为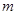
，带电荷量为
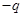的粒子，以速度
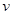从O点射入磁场，角
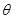已知，粒子重力不计，求：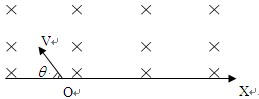
(1)粒子在磁场中运动的时间；
(2)粒子离开磁场的位置与O点间的距离。
在平直公路上，以速度v0 ="12" m/s匀速前进的汽车，遇紧急情况刹车后，轮胎停止转动在地面上滑行，经过时间t=1.5s汽车停止，当地的重力加速度g取10 m/s2.求：
（1）刹车时汽车加速度a的大小；
（2）刹车时汽车轮胎与地面间的动摩擦因数μ.