如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求: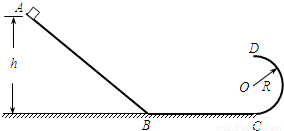
(1)小物块通过B点时速度vB的大小;
(2)试通过计算说明,小物块能否通过圆形轨道的最高点D。
跳台滑雪是勇敢者的运动,它是利用依山势特别建造的跳台进行的。运动员穿着专用滑雪板,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆。这项运动极为壮观。设一位运动员由山坡顶的A点沿水平方向飞出,到山坡上的B点着陆。如图所示,已知运动员水平飞出的速度为v0 = 20m/s,山坡倾角为θ= 37°,山坡可以看成一个斜面。(g = 10m/s2,sin37º= 0.6,cos37º= 0.8)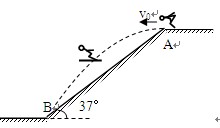
求:(1)运动员在空中飞行的时间t;
(2)AB间的距离s。
神舟六号载人飞船在绕地球飞行了5 圈后变轨,轨道变为距地面高度为h 的圆形轨道.已知地球半径为 ,地面附近的重力加速度为
,地面附近的重力加速度为 .求:
.求:
(1)飞船在圆轨道上运行的速度 ;
;
(2)飞船在圆轨道上运行的周期 .
.
一细绳与水桶相连,水桶中装有水,水桶与细绳一起在竖直平面内做圆周运动,如图所示,水的质量m=0.5kg,水的重心到转轴的距离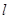 =50cm。(取g=10m/s2,不计空气阻力)
=50cm。(取g=10m/s2,不计空气阻力)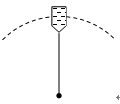
(1)若在最高点水不流出来,求桶的最小速率;
(2)若在最高点水桶的速率v=3m/s,求水对桶底的压力大小。
如图所示,AB为斜面轨道,与水平方向成45°角,BC为水平轨道,两轨道在B处通过一段小圆弧相连接,一质量为m的小物块,自轨道AB的A处从静止开始沿轨道下滑,最后停在轨道上的C点,已知A点高h,物块与轨道间的滑动摩擦系数为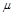 ,求:
,求:
(1)在整个滑动过程中摩擦力所做的功
(2)施加一平行于接触面外力使物块缓慢地沿原路回到A点所需做的功
(3)小物块经过AB段与BC段时间之比
如图所示,宇航员站在某星球表面上的斜面顶端A处,沿水平方向以初速度V0抛出一个小球。经时间t小球落在斜面上的某一点B处。设空气阻力不计,该星球半径为R,万有引力常数为G。求该星球的质量M为多少(斜面倾角为θ)