如图,在四棱锥P-ABCD中,平面PAD⊥底面 ABCD,侧棱PA=PD=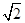 ,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)线段AD上是否存在点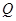 ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为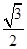 ?若存在,求出
?若存在,求出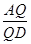 值;若不存在,请说明理由.
值;若不存在,请说明理由.
一盒中装有分别标记着1,2,3,4数字的4个小球,每次从袋中取出一只球,设每只小球被取出的可能性相同.(I)若每次取出的球不放回盒中,现连续取三次球,求恰好第三次取出的球的标号为最大数字的球的概率;(II)若每次取出的球放回盒中,然后再取出一只球,现连续取三次球,这三次取出的球中标号最大数字为 ,求
,求 的概率分布列与期望.
的概率分布列与期望.




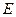






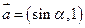


⑴若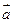 ∥
∥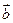 ,求
,求 的值;
的值;
⑵若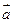

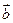
 ,求
,求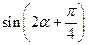 的值
的值
排一张有5个歌唱节目和4个舞蹈节目的演出节目单.
(1)任何两个舞蹈节目不相邻的排法有多少种?
(2)歌唱节目与舞蹈节目间隔排列的方法有多少种?
某一天的课程表要排入政治、语文、数学、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,那么共有多少种不同的排课程表的方法?