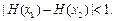已知抛物线C: ,点
,点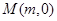 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
(1)若 ,且直线
,且直线 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线 绕点M如何转动,
绕点M如何转动, 恒为定值?
恒为定值?
本大题满分12分)
在△ABC中,
(I)求B,
(Ⅱ)若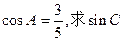 的值。
的值。
已知数列 是公差为
是公差为
 的等差数列,数列
的等差数列,数列 是公比为
是公比为 的(q∈R)的等比数列,若函数
的(q∈R)的等比数列,若函数 ,且
,且
 ,
, ,
, ,
,
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,对一切
,对一切 ,都有
,都有 成立,求
成立,求
本题共有2个小题,第1小题满分8分,第2小题满分8分.已知函数 (其中
(其中 且
且 ,
, 为实数常数).
为实数常数).
(1)若 ,求
,求 的值(用
的值(用 表示);
表示);
(2)若 且
且 对于
对于 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用 表示).
表示).
由于卫生的要求游泳池要经常换水(进一些干净的水同时放掉一些脏水), 游泳池的水深经常变化,已知泰州某浴场的水深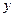 (米)是时间
(米)是时间 ,(单位小时)的函数,记作
,(单位小时)的函数,记作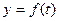 ,下表是某日各时的水深数据
,下表是某日各时的水深数据
| t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
| y(米) |
2 5 5 |
2 0 0 |
1 5 5 |
2 0 0 |
2 49 49 |
2 |
1 51 51 |
1 99 99 |
2 5 5 |
经长期观测的曲线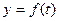 可近似地看成函数
可近似地看成函数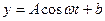
(Ⅰ)根据以上数据,求出函数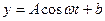 的最小正周期T,振幅A及函数表达式;
的最小正周期T,振幅A及函数表达式;
(Ⅱ)依据规定,当水深大于2米时才对游泳爱好者开放,请依据(1)的结论,判断一天内的上午8 00至晚上20
00至晚上20 00之间,有多少时间可供游泳爱好者进行运动
00之间,有多少时间可供游泳爱好者进行运动
(本小题满分16分)已知二次函数g(x)对任意实数x都满足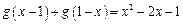 ,且
,且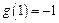 .令
.令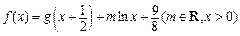 .
.
(1)求 g(x)的表达式;
(2)若 使
使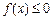 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)设 ,
,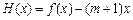 ,证明:对
,证明:对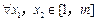 ,恒有
,恒有