某食品厂从生产的袋装食品中随机抽样检测20袋的质量是否符合标准质量，超过或不足的质量分别用正、负数表示，例如＋2表示该袋食品超过标准质量2g，现记录如下：
| 与标准质量的误差（g） |
－5 |
－2 |
0 |
+1 |
+3 |
+6 |
| 袋数 |
5 |
3 |
3 |
4 |
2 |
3 |
（1）在抽取的样品中，最重的那袋食品的质量比最轻的那袋多了多少克？
（2）若标准质量为100g／袋，则这次抽样检测的总质量是多少克？
如图，正△ABC的边长为6，点D是BC边上一点，连结AD，将AD绕点A顺时针旋转60°得AE，连结DE交AB于点F．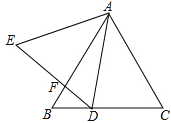
（1）填空：若∠BAD=20°，则∠BDF= °；
（2）若当点D在线段BC上运动时（不与B、C两点重合），设BD=x，BF=y，试求y与x之间的函数关系式；
（3）若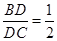
，请求出AE的长．
某商场以每件若干元的价格购进一批商品，当每件商品售价为360元时，每月可售出50件，每件获利20%，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出6件．
（1）降价前商场每月销售该商品的利润是多少元？
（2）要使商场每月销售这种商品的利润达到5500元，且更有利于减少库存，则每件商品应降价多少元？
如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，过点C作CF∥BE交DE的延长线于F．
（1）求证：四边形BCFE是菱形；
（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．
如图，把圆形转盘A平均4等份、圆形转盘B平均3等份，并在每一个小区域内标上数字．欢欢、乐乐两个人玩转盘游戏，游戏规则如下：同时转动两个转盘，当转盘停止时，若指针所指两区域的数字之积为奇数，则欢欢胜；若指针所指两区域的数字之积为偶数，则乐乐胜；若有指针落在分割线上，则无效，重转．
（1）若单独自由转动A盘，当它停止转动时，指针指向奇数区的概率是 ．
（2）用列表或画树状图的方法求出欢欢获胜的概率．
解方程：2x2-9x+8=0．