一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
计算:(本题每小题4分,满分8分)
(1)求右式中x的值:4(x+1 =64
=64
(2)
已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.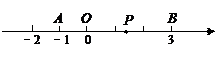
(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由.
(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
学校植物园沿路护栏纹饰部分设计成若干个相同的菱形图案,每增加一个菱形图案,纹饰长度就增加d cm,如图所示.已知每个菱形的横向对角线长为30cm.
(1)若该纹饰要231个菱形图案,试用含d的代数式表示纹饰的长度L;
当d=26时,求该纹饰的长度L;
(2)当d=20时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?
在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到该商品售价13%的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机,两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.试求:
(1)A型洗衣机和B型洗衣机的售价各是多少元?
(2)小李和小王购买洗衣机除财政补贴外实际各付款多少元?
如图,直线AB、CD相交于O,∠BOC=800,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)试说明:OF平分∠AOD