问题提出:如图①,将一张直角三角形纸片 折叠,使点
折叠,使点 与点
与点 重合,这时
重合,这时 为折痕,
为折痕, 为等腰三角形;再继续将纸片沿
为等腰三角形;再继续将纸片沿 的对称轴
的对称轴 折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
知识运用:
(1)如图②,正方形网格中的 能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的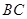 为一边,画出一个斜三角形
为一边,画出一个斜三角形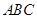 ,使其顶点
,使其顶点 在格点上,且
在格点上,且 折成的“叠加矩形”为正方形;
折成的“叠加矩形”为正方形;
(3)若一个锐角三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?结合图③,说明理由。
拓展应用:
(4)如果一个四边形一定能折成"叠加矩形",那么它必须满足的条件是什么?
学习了函数的知识后,数学活动小组到文具店调研一种进价为每支2元的活动笔的销售情况。调查后发现,每支定价3元,每天能卖出100支,而且每支定价每下降0.1元,其销售量将增加10支。但是物价局规定,该活动笔每支的销售利润不能超过其进价的40%。设每支定价x元,每天的销售利润为y元。
(1)求每天的销售利润为y与每支定价x之间的函数关系式;
(2)如果要实现每天75元的销售利润,那么每支定价应为多少元?
(3)当每支定价为多少元时,可以使这种笔每天的销售利润最大?
如图, △ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1∶2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
益家果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千 克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利 还是亏损?盈利或亏损了多少元?