对于函数
，现有下列命题：①函数
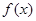是奇函数；②函数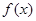的最小正周期是
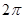；③点
是函数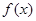的图象的一个对称中心；④函数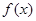在区间
上单调递增，其中是真命题的为（ ）
| A．②④ | B．①④ | C．②③ | D．①③ |
已知双曲线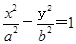
（a>0，b>0）的渐近线与圆
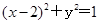相交，则双曲线的离心率的取值范围是
| A．（1，3） | B．（ ，+∞） |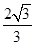
| C．（1，） |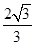
D．（3，+∞） |
设P是椭圆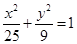
上一点，M、N分别是圆（x＋4）2＋y2＝1和（x－4）2＋y2＝1上的点，则|PM|＋|PN|的最小值、最大值分别为
| A．9，12 | B．8，11 | C．8，12 | D．10，12 |
双曲线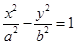
（a>0，b>0）的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点（1，2）在“上”区域内，则双曲线离心率e的取值范围是
A．（1， ] |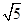
B．（1，） |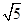
C．（1，2] |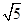
D．（1，2） |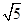
已知椭圆
的右焦点为
，过点
的直线交椭圆于
两点．若
的中点坐标为
，则
的方程为
A． |
B． |
C． |
D． |
设
是椭圆
的左、右焦点，
为直线
上一点，
是底角为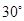
的等腰三角形，则
的离心率为
A． |
B． |
C． |
D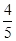． |