已知中心在原点,焦点在坐标轴上的双曲线与圆x2+y2=17有公共点A(1,﹣4),且圆在A点的切线与双曲线的渐近线平行,则双曲线的离心率为( )
A. |
B. |
C. 或 或 |
D.以上都不对 |
若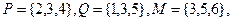 则
则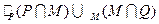 = ( )
= ( )
| A.{2,4} | B.{2,4,6} | C.{1,2,4,6} | D.{1,2,3,4 ,5} ,5} |
函数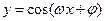
 为奇函数,该函数的部分图像如右图所表示,
为奇函数,该函数的部分图像如右图所表示, 、
、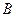 分别为最高点与最低点,并且两点间的距离为
分别为最高点与最低点,并且两点间的距离为 ,则该函数的一条对称轴为
,则该函数的一条对称轴为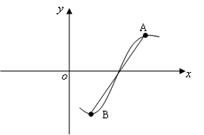
A. |
B. |
C.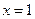  |
D. |
等腰直角三角形ABC中,A= ,AB=AC=2,M是BC的中点,P点在
,AB=AC=2,M是BC的中点,P点在 ABC内部或其边界上运动,则即
ABC内部或其边界上运动,则即 ·
· 的取值范围是
的取值范围是
| A.[-l,0] | B.[1,2] | C.[-2,-1] | D.[-2,0] |
定义在R上的可导函数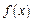 满足
满足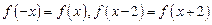 ,且当
,且当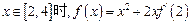 ,则
,则 的大小关系是
的大小关系是
A.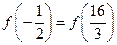 |
B.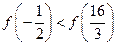 |
C.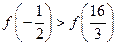 |
D.不确定 |
F1、F2分别是双曲线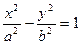 的左、右焦点,A是其右顶点,过F2作
的左、右焦点,A是其右顶点,过F2作 轴的垂线与双曲线的一个交点为P,G是
轴的垂线与双曲线的一个交点为P,G是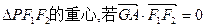 ,则双曲线的离心率是
,则双曲线的离心率是
| A.2 | B.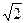 |
C.3 | D.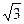 |