设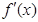 是函数
是函数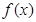 的导函数,将
的导函数,将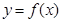 和
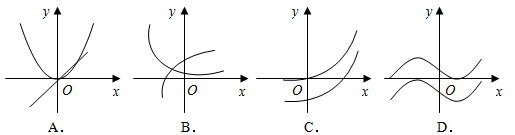
和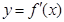 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )
设函数 在R上可导,其导函数为
在R上可导,其导函数为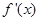 ,且函数
,且函数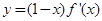 的图象如图所示,则下列结论中一定成立的是 ()
的图象如图所示,则下列结论中一定成立的是 ()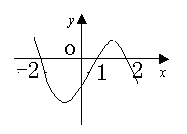
A.函数 有极大值 有极大值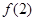 和极小值 和极小值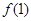 |
B.函数 有极大值 有极大值 和极小值 和极小值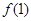 |
C.函数 有极大值 有极大值 和极小值 和极小值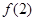 |
D.函数 有极大值 有极大值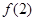 和极小值 和极小值 |
有一段“三段论”,推理是这样的:对于可导函数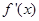 ,如果
,如果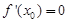 ,那么
,那么 是函数
是函数 的极值点,因为
的极值点,因为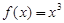 在
在 处的导数值
处的导数值 ,所以
,所以 是函数
是函数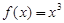 的极值点.以上推理中()
的极值点.以上推理中()
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
函数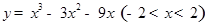 有()
有()
A.最大值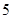 ,最小值-22 ,最小值-22 |
B.最大值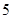 ,最小值-2 ,最小值-2 |
C.最大值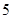 ,无最小值 ,无最小值 |
D.最小值 ,无最大值 ,无最大值 |
用反证法证明命题“若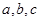 都是正数,则
都是正数,则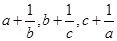 三数中至少有一个不小于
三数中至少有一个不小于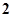 ”,提出的假设是()
”,提出的假设是()
A.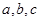 不全是正数 不全是正数 |
B.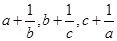 至少有一个小于 至少有一个小于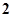 |
C.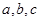 都是负数 都是负数 |
D.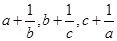 都小于2 都小于2 |
已知函数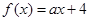 ,若
,若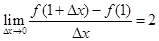 ,则实数
,则实数 的值为()
的值为()
A.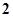 |
B. |
C. |
D. |