如图,将一块直角三角形纸板的直角顶点放在C(1, )处,两直角边分别与
)处,两直角边分别与 轴平行,纸板的另两个顶点
轴平行,纸板的另两个顶点 恰好是直线
恰好是直线 与双曲线
与双曲线 的交点.
的交点.
(1)求 和
和 的值;
的值;
(2)设双曲线 在
在 之间的部分为
之间的部分为 ,让一把三角尺的直角顶点
,让一把三角尺的直角顶点 在
在 上滑动,两直角边始终与坐标轴平行,且与线段
上滑动,两直角边始终与坐标轴平行,且与线段 交于
交于 两点,请探究是否存在点
两点,请探究是否存在点 使得
使得 ,写出你的探究过程和结论.
,写出你的探究过程和结论.
一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同.进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x如图2所示.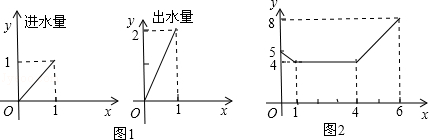
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.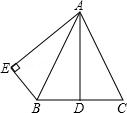
(1)求证:AD=AE.
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
(1)已知2x+1的平方根为±5,求5x+4的立方根.
(2)已知x+y的算术平方根是3,(x-y)2=9,求xy的值.
已知点P(x,y)是第一象限内的一个动点,且满足x+y=4.请先在所给的平面直角坐标系中画出函数y=2x+1的图象,该图象与x轴交于点A,然后解答下列问题: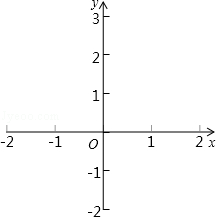
(1)利用所画图象,求当-1≤y≤3时x的取值范围;
(2)若点P正好也在直线y=2x+1上,求点P的坐标;
(3)设△OPA的面积为S,求S关于点P的横坐标x的函数解析式.
如图,四边形ABCD是长方形.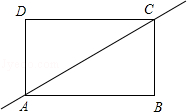
(1)作△ABC关于直线AC对称的图形;
(2)试判断(1)中所作的图形与△ACD重叠部分的三角形形状,并说明理由.