如图,一次函数 的图象与反比例函数
的图象与反比例函数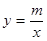 的图象交于P(-2,1)、Q(1,
的图象交于P(-2,1)、Q(1,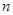 )两点.
)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的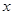 的取值范围.
的取值范围.
如图(1),在平面直角坐标系中,抛物线 与y轴交于点A,与x轴交于点 ,且经过点B(8,4),连接AB,BO,作 于点M,将 沿y轴翻折,点M的对应点为点N.解答下列问题:
(1)抛物线的解析式为 ,顶点坐标为 ;
(2)判断点N是否在直线AC上,并说明理由;
(3)如图(2),将图(1)中 沿着OB平移后,得到 .若DE边在线段OB上,点F在抛物线上,连接AF,求四边形 的面积.
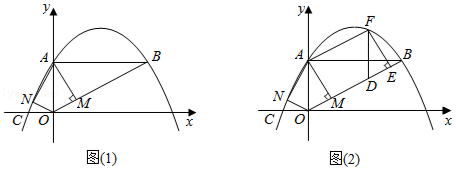
如图,已知AB是⊙O的直径,⊙O经过 的直角边DC上的点F,交AC边于点E,点F是弧EB的中点, ,连接AF.
(1)求证:直线CD是⊙O切线.
(2)若 , ,求 的值.

在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢?我们可以用下面的方式来解决问题.
用点A1、A2、A3…A48分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:

(1)填写上图中第四个图中y的值为 ,第五个图中y的值为 .
(2)通过探索发现,通电话次数y与该班级人数x之间的关系式为 ,当 时,对应的y= .
(3)若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?
某单位计划购买甲、乙两种品牌的消毒剂,乙种品牌消毒剂每瓶的价格比甲种品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲种品牌消毒剂的数量与用400元购买乙种品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该单位从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙种品牌消毒剂?
勤劳是中华民族的传统美德,学校要求学们在家帮助父母做一些力所能及的家务.在学期初,小丽同学随机调查了七年级部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别: , , , , .并将调查结果绘制了如图两幅不完整的统计图:

根据统计图提供的作息,解答下列问题:
(1)本次共调查了 名学生;
(2)根据以上信息直接在答题卡上补全条形统计图;
(3)扇形統计图中m= ,类别D所对应的扇形圆心角α的度数是 度;
(4)若该校七年级共有400名学生,根据抽样调查的结果,估计该校七年級有多少名学生寒假在家做家务的总时间不低于20小时?