八年级数学课上,朱老师出示了如下框中的题目.
小聪与同桌小明讨论后,进行了如下解答:
(1)特殊情况·探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE_________DB(填“>”,“<”或“=”).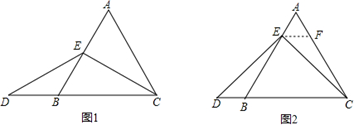
(2)特例启发·解答题目
解:题目中, AE与DB的大小关系是:AE______DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论·设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=1,则CD=(请你直接写出结果).
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长分别为6m、8 m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边长的直角三角形.请你设计出所有合适的方案,画出草图,并求出扩建后的等腰三角形花圃的面积. 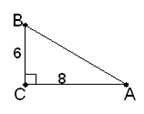
已知:如图,在△ABC中,∠BAC=90°,BD平分∠ABC,DE⊥BC于E.
证明:BD垂直平分AE.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B.
求证:AD+AB=BE.
如图,已知CD="6" m,AD="8" m,∠ADC=90°,BC="24" m,AB="26" m.求图中阴影部分的面积.