在数学活动课上，九年级（1）班数学兴趣小组的同学们测量校园内一棵大树的高度，设计的方案及测量数据如下：
（1）在大树前的平地上选择一点
，测得由点看大树顶端
的仰角为30°；
（2）在点和大树之间选择一点
（
在同一条直线上），测得由点看大树顶端的仰角恰好为45°；
（3）量出
两点间的距离为
．请你根据以上数据求出大树
的高度．（结果保留3个有效数字）
计算：（1）
（2）先化简，后计算：
，其中
.
如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3）．反比例函数
的函数图象经过点D，点P是一次函数y=kx+3-3k（k≠0）的图象与该反比例函数图象的一个公共点．
（1）求反比例函数的解析式；
（2）通过计算，说明一次函数y=kx+3-3k（k≠0）的图象一定过点C；
（3）对于一次函数y=kx+3-3k（k≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围（不必写出过程）．
如图所示，已知两点A（-1，0），B（4，0），以AB为直径的半圆P交y轴于点C．
（1）求经过A、B、C三点的抛物线的解析式；
（2）设弦AC的垂直平分线交OC于D，连接AD并延长交半圆P于点E，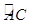
与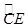
相等吗？请证明你的结论；
（3）设点M为x轴负半轴上一点，OM=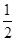
AE，是否存在过点M的直线，使该直线与（1）中所得的抛物线的两个交点到y轴的距离相等？若存在，求出这条直线对应函数的解析式；若不存在．请说明理由．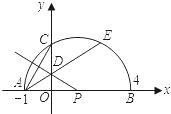
已知⊙O的半径为12cm，弦AB=16cm．
（1）求圆心O到弦AB的距离；
（2）如果弦AB的长度保持不变，两个端点在圆周上滑动，那么弦AB的中点形成什么样的图形？
如图，△ABC是等边三角形，⊙O过点B，C，且与BA，CA的延长线分别交于点D，E，弦DF∥AC，EF的延长线交BC的延长线于点G．
（1）求证：△BEF是等边三角形；
（2）若BA=4，CG=2，求BF的长．