阅读下面材料：
小腾遇到这样一个问题：如下图①，在△ABC中，点D在线段BC上，∠BAD=75°，∠CAD=30°，AD=2，BD=2DC，求AC的长．
小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如上图②）．
请回答：∠ACE的度数为____，AC的长为____．
参考小腾思考问题的方法，解决问题：
如下图③，在四边形ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2ED，求BC的长．
③
已知x、y满足
+｜x－2y+2｜＝0，求x－
y的平方根.
先化简，再求值：[（2xy－3）（2xy＋3）＋（xy＋3）2]÷xy，
其中x=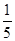
，y＝－2.
因式分解：3a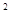
－6a+3
图是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．
（1）证明：△ABE≌△CBD；
（2）图中存在多对相似三角形，请你找出一对进行证明，并求出其相似比（不添加辅助线，不找全等的相似三角形）；
（3）小红发现AM=MN=NC，请证明此结论；
（4）求线段BD的长．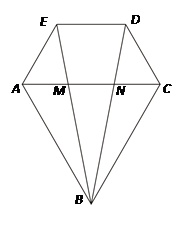
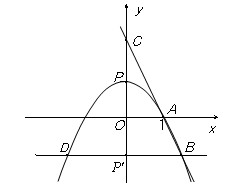
如图，已知抛物线经过定点A（1，0），它的顶点P是y轴正半轴上的一个动点，
P点关于x轴的对称点为P′，过P′ 作x轴的平行线交抛物线于B、D两点（B点在y轴右
侧），直线BA交y轴于C点．按从特殊到一般的规律探究线段CA与CB的比值：
（1）当P点坐标为（0，1）时，写出抛物线的解析式并求线段CA与CB的比值；
（2）若P点坐标为（0，m）时（m为任意正实数），线段CA与CB的比值是否与⑴所求的比值相同？请说明理由．