如图,在平行四边形ABCD中,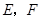 为
为 上两点,且
上两点,且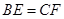 ,
,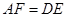 .
.
求证:(1)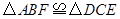 ;
;
(2)四边形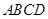 是矩形.
是矩形.
(1)解方程: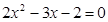 ;
;
(2)解不等式组:
计算:
(1)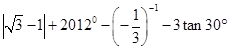
(2)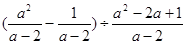
如图①,已知二次函数的解析式是y=ax2+bx(a>0),顶点为A(1,-1).
(1)a=;
(2)若点P在对称轴右侧的二次函数图像上运动,连结OP,交对称轴于点B,点B关于顶点A的对称点为C,连接PC、OC,求证:∠PCB=∠OCB;
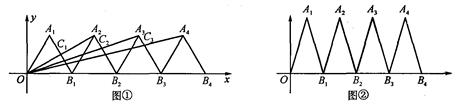
(3)如图②,将抛物线沿直线y=-x作n次平移(n为正整数,n≤12),顶点分别为A1,A2,…,An,横坐标依次为1,2,…,n,各抛物线的对称轴与x轴的交点分别为D1,D2,…,Dn,以线段AnDn为边向右作正方形AnDnEnFn,是否存在点Fn恰好落在其中的一个抛物线上,若存在,求出所有满足条件的正方形边长;若不存在,请说明理由.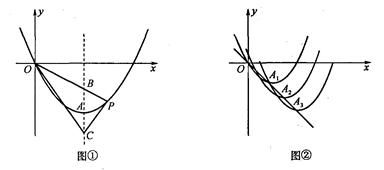
好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.