如图所示,电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角,导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T,方向垂直导轨平面向上的匀强磁场,边界ef、gh之间的距离D=1.4m。现将质量m=0.1kg、电阻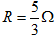 的导体棒P、Q相隔Δt=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s。已知重力加速度g=10m/s2,sin37°=0.6,求
的导体棒P、Q相隔Δt=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s。已知重力加速度g=10m/s2,sin37°=0.6,求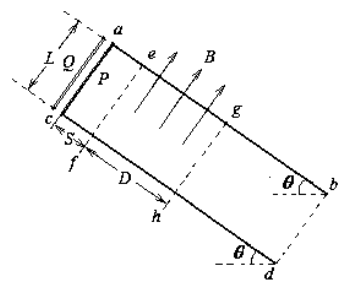
(1)导轨顶端与磁场上边界ef之间的距离S;
(2)从导体棒P释放到Q穿出磁场的过程,回路中产生的焦耳热Q总。
普朗克常量
 ,铝的逸出功
,铝的逸出功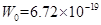
 ,现用波长
,现用波长 的光照射铝的表面(结果保留三位有效数字)。
的光照射铝的表面(结果保留三位有效数字)。
(1)求光电子的最大初动能;
(2)若射出的一个具有最大初动能的光电子正对一个原来静止的电子运动,求在此运动过程中两电子电势能增加的最大值(电子所受的重力不计)。
一列沿x轴传播的横波如图所示,波长λ="8" m,实线表示t1=0时刻的波形图,虚线表示t2="0.005" s时刻的波形图.求:
(1)波速多大?
(2)若2T>t2-t1>T,波速又为多大?
(3)若t2-t1>T,并且波速为3600 m/s,则波沿哪个方向传播?
如图所示实线是某时刻的波形图像,虚线是经过0.2s时的波形图像。求: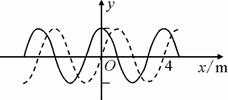
(1)波传播的可能距离;
(2)可能的周期(频率);
(3)可能的波速;
(4)若波速是35m/s,求波的传播方向;
(5)若0.2s小于一个周期时,求传播的距离、周期(频率)、波速。
有一种沙漠蝎子既没有眼睛,也没有耳朵,它捕食猎物靠的是一种地震仪式的本领。它有八条腿,趴伏时大致对称地放置在躯体四周(如图所示),不远处的小虫一有骚动,就会在沙面上引起一阵地震波。蝎子从哪只腿先感到地震波就能判断小虫所在的方向,并从P波和S波到达的时间差就可以“算出”小虫到它的距离,方位和距离都知道了,它就能扑上去捕获小虫了。已知P波速度为150 m/s,S波速度为50 m/s。如果两波到达沙漠蝎子的时间差为3.5 ×10-3s,则小虫离它的距离多大?
弹簧振子以O点为平衡位置在B.C两点间做简谐振动,在t=0时刻,振子从O.B间的P点以速度v向B点运动;在t=0.20s时,振子速度第一次变为―v;在t=0.50s时,振子速度第二次变为―v。
(1)求弹簧振子的振动周期T。
(2)若B.C之间的距离为25cm,求振子在4.00s内通过的路程。
(3)若B.C之间的距离为25 cm,从平衡位置计时,写出弹簧振子位移的表达式,并画出弹簧振子的振动图象。