将抛物线y=2x2-12x+16绕它的顶点旋转180°,所得的解析式是( )
| A.y=-2x2-12x+16 | B.y=-2x2+12x-16 |
| C.y=-2x2+12x-19 | D.y=-2x2+12x-20 |
已知点(-1,y1),(2,y2),(3,y3)在反比例函数y= 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y1>y2 | D.y2>y3>y1 |
已知抛物线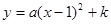 与x轴交与点A(m,0),B(4,0),则 A、B两点之间的距离是()
与x轴交与点A(m,0),B(4,0),则 A、B两点之间的距离是()
A、2
B、4
C、6
D、8
要得到二次函数 的图象,则需将
的图象,则需将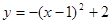 的图象()
的图象()
| A.向右平移两个单位; | B.向下平移1个单位; |
C.关于 轴做轴对称变换; 轴做轴对称变换; |
D.关于 轴做轴对称变换; 轴做轴对称变换; |
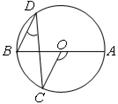
如图,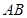 是⊙
是⊙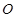 直径,
直径,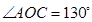 ,则
,则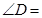 ()
()
A.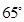 |
B.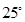 |
C. |
D.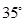 |