不等式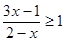 的解集是()
的解集是()
A. |
B.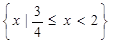 |
C.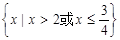 |
D. |
如右图所示,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭
圆外的黄豆数为96颗,以此实验数据为依据可以估计出椭圆的面积约为( )
| A.7.68 | B.16.32 |
| C.17.32 | D.8.68 |
已知A(2,-2),B(4,3),向量p的坐标为(2k-1,7)且p∥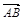 ,则k的值为 ( )
,则k的值为 ( )
A.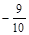 |
B.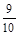 |
C.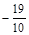 |
D.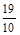 |
设a 、b是两条不同的直线,α、β是两个不同的平面,则下列四个命题
①若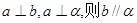 ②若
②若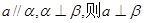
③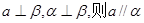 ④
④
其中正确的命题的个数是()
| A.0个 | B.1个 | C.2个 | D.3个 |
若角 的终边过点(sin30o,-cos30o),则sin
的终边过点(sin30o,-cos30o),则sin 等于( )
等于( )
A. |
B.- |
C.-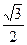 |
D.- |