从1到9的九个数字中任取三个偶数四个奇数,问:
(Ⅰ)能组成多少个没有重复数字的七位数?
(Ⅱ)上述七位数中三个偶数排在一起的概率?
(Ⅲ)在(Ⅰ)中任意两偶数都不相邻的概率?
一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为
40秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3)不是红灯
化简:
(1)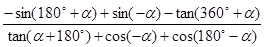

(2)
已知函数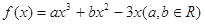 ,在点
,在点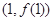 处的切线方程为
处的切线方程为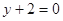 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有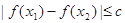 ,求实数
,求实数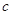 的最小值;
的最小值;
(Ⅲ)若过点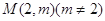 ,可作曲线
,可作曲线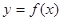 的三条切线,求实数
的三条切线,求实数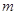 的取值范围.
的取值范围.
已知椭圆C: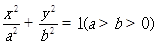 的离心率为
的离心率为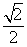 ,其中左焦点
,其中左焦点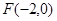 .
.
(Ⅰ)求出椭圆C的方程;
(Ⅱ) 若直线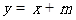 与曲线C交于不同的A、B两点,且线段AB的中点M在圆
与曲线C交于不同的A、B两点,且线段AB的中点M在圆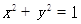 上,求m的值.
上,求m的值.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,
且AC=AD=CD=DE=2,AB=1.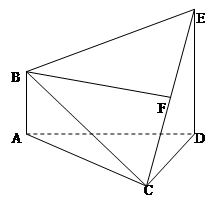
(Ⅰ)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(Ⅱ)求多面体ABCDE的体积.