若直线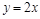
上存在点(x，y)满足约束条件
，则实数m的最大值为（ ）
A． |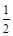
B．1 | C． |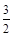
D．2 |
用数学归纳法证明12+22+…+（n﹣1）2+n2+（n﹣1）2+…+22+12═
时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（）
| A．（k+1）2+2k2 | B．（k+1）2+k2 |
| C．（k+1）2 | D． |
在用数学归纳法证明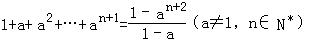
时，在验证当n=1时，等式左边为（）
| A．1 | B．1+a | C．1+a+a2 | D．1+a+a2+a3 |
已知n为正偶数，用数学归纳法证明
时，若已假设n=k（k≥2）为偶数）时命题为真，则还需要用归纳假设再证n=（）时等式成立．
| A．n=k+1 | B．n=k+2 | C．n=2k+2 | D．n=2（k+2） |
用数学归纳法证明：1+2+22+…2n﹣1=2n﹣1（n∈N）的过程中，第二步假设当n=k时等式成立，则当n=k+1时应得到（）
| A．1+2+22+…+2k﹣2+2k+1﹣1 |
| B．1+2+22+…+2k+2k+1=2k﹣1+2k+1 |
| C．1+2+22+…+2k﹣1+2k+1=2k+1﹣1 |
| D．1+2+22+…+2k﹣1+2k=2k﹣1+2k |
证明1+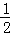
+…+
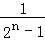
（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（）
| A．1项 | B．k﹣1项 | C．k项 | D．2k项 |