某高中数学竞赛培训在某学段共开设有初等代数、平面几何、初等数论和微积分初步共四门课程,要求初等数论、平面几何都要合格,且初等代数和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格.现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同(见下表),且每一门课程是否合格相互独立.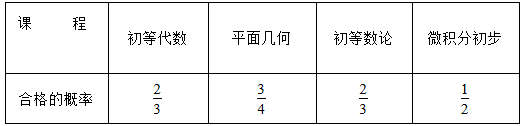
(Ⅰ)求甲同学取得参加数学竞赛复赛的资格的概率;
(Ⅱ)记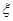 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求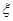 的分布列及期望
的分布列及期望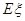 .
.
(本小题满分12分)
已知 =(cos
=(cos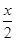 +sin
+sin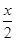 ,-sin
,-sin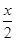 ),
), =(cos
=(cos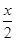 -sin
-sin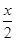 ,2cos
,2cos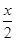 ).
).
(1)设f(x)= ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈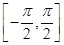 ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
(本小题满分12分)
在△ABC中,已知B=45°,D是BC边上的一点,AD="10," AC=14,DC=6,求AB的长.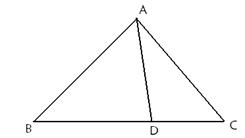
(本小题满分12分)
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
(本小题满分10分)
求值: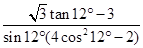 .
.
已知函数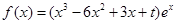 ,
, .
.
(1)若函数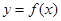 依次在
依次在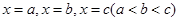 处取到极值.
处取到极值.
①求 的取值范围;
的取值范围;
②若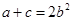 ,求
,求 的值.
的值.
(2)若存在实数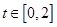 ,使对任意的
,使对任意的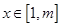 ,不等式
,不等式 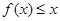 恒成立.求正整数
恒成立.求正整数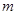 的最大值
的最大值