如图所示，两根足够长平行金属导轨MN、PQ固定在倾角θ=37°的绝缘斜面上，顶部接有一阻值R=3Ω的定值电阻，下端开口，轨道间距L="1" m。整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直斜面向上。质量m=1kg的金属棒ab置于导轨上，ab在导轨之间的电阻r=1Ω，电路中其余电阻不计。金属棒ab由静止释放后沿导轨运动时始终垂直于导轨，且与导轨接触良好。不计空气阻力影响。已知金属棒ab与导轨间动摩擦因数μ=0.5，sin37°=0.6，cos37°=0.8，取g=10m/s2。
（1）求金属棒ab沿导轨向下运动的最大速度vm；
（2）求金属棒ab沿导轨向下运动过程中，电阻R上的最大电功率PR；
（3）若从金属棒ab开始运动至达到最大速度过程中，电阻R上产生的焦耳热总共为1.5J，求流过电阻R的总电荷量q。
做自由落体运动的小球，从离地20米处下落（g取10m/s2）,则
（1）小球着地时速度是多大？
（2）小球在最后1秒的平均速度为多大？
如图所示，在足够长的光滑绝缘水平直线轨道上方h高度的P点，固定电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点)，从轨道上的A点以初速度v0沿轨道向右运动，当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零)，PA连线与水平轨道的夹角为60°，试求：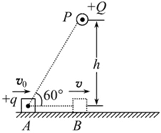
(1)物块在A点时受到的轨道的支持力大小.
(2)点电荷+Q产生的电场在B点的电势大小.
利用电场和磁场，可以将比荷不同的离子分开，这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场，A处有一狭缝.离子源产生的离子经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场，运动到GA边，被相应的收集器收集.整个装置内部为真空.
已知被加速的两种正离子的质量分别是m1和m2(m1>m2)，电荷量均为q.加速电场的电势差为U，离子进入电场时的初速度可以忽略.不计重力，也不考虑离子间的相互作用.
(1)求质量为m1的离子进入磁场时的速率v1；
(2)当磁感应强度的大小为B时，求两种离子在GA边落点的间距.
民用航空客机的机舱一般都设有紧急出口，飞机发生意外情况着陆后，打开紧急出口的舱门，会自动生成一个气囊（由斜面AC部分和水平面CD部分构成的）。如图所示为某气囊斜面，机舱离底端的竖直高度AB=3.0m，斜面长AC=5.0m，斜面与水平面CD段间有一段小圆弧平滑连接。一个质量m=60kg的旅客从气囊上由静止开始滑下，最后滑上水平面上的某点静止。已知旅客与气囊斜面部分及水平面部分的动摩擦因数均为
=0.5。（不计空气阻力，g=10m/s2，sin37°=0.6和cos37°=0.8）。（计算结果可保留根号）
求：(1) 人在斜面上运动时的加速度大小；
(2)人滑到斜面底端C时的速度大小；
(3)人滑过C点后还要多久才能停下。
一列火车在准备进站前一段时间保持匀速行驶，准备进站时关闭气阀（动力系统）让车滑行，火车滑行了240m时，速度恰为关闭气阀时速度的一半，此后，又继续滑行，20s后停止在车站，设火车在关闭气阀后滑行过程中加速度始终保持不变，求：
（1）火车关闭气阀后滑行的加速度大小；
（2）火车从关闭气阀到停止滑行的总时间。