如图所示,宽度为L的粗糙平行金属导轨PQ和P′Q′倾斜放置,顶端QQ′之间连接一个阻值为R的电阻和开关S,底端PP′处与一小段水平轨道用光滑圆弧相连。已知底端PP′离地面的高度为h,倾斜导轨处于垂直于导轨平面的匀强磁场(图中未画出)中。若断开开关S,一根质量为m、电阻为r、长也为L的金属棒从AA′处由静止开始滑下,金属棒落地点离PP′的水平距离为x1;若闭合开关S,该金属棒仍从AA′处由静止开始滑下,则金属棒落地点离PP′的水平距离为x2。不计导轨电阻,忽略金属棒经过PP′处的机械能损失,已知重力加速度为g,求: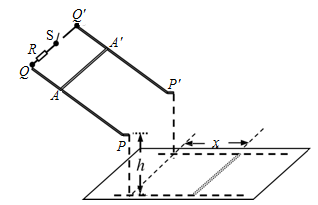
(1)开关断开时,金属棒离开底端PP′的速度大小;
(2)开关闭合时,在下滑过程金属棒中产生的焦耳热。
(3)开关S仍闭合,金属棒从比AA′更高处由静止开始滑下,水平射程仍为x2,请定性说明金属棒在倾斜轨道上运动的规律。
一列火车共有n节车厢且均停在光滑的长直轨道上,各车厢间距相等,间距总长为a.若第一节车厢以速度v向第二节车厢运动,碰撞时间极短且碰后不分开,然后一起向第三节车厢运动,……依次直到第n节车厢.试求:
(1)火车的最后速度是多大?
(2)整个过程经历的时间是多长?
在h高处,以初速度v0向水平方向抛出一个小球,不计空气阻力,小球着地时速度大小为多少?
将质量m=2kg的一块石头从离地面H=2m高处由静止开始释放,落入泥潭并陷入泥中h=5cm深处,不计空气阻力,求泥对石头的平均阻力。(g取10m/s2)
一架喷气式飞机,质量m=5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力。
一个质量为2kg的小球从45m的高处自由下落,求2秒内的平均功率是多少?2秒末的瞬时功率是多少?