如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.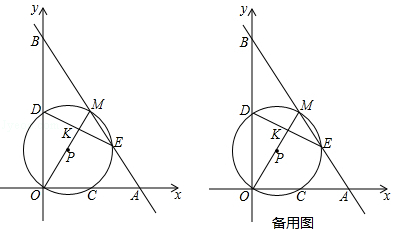
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若 ,求∠OBA的度数.
,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1), ,直接写出y关于x的函数解析式.
,直接写出y关于x的函数解析式.
某校师生积极为汶川地震灾区捐款捐物,在得知灾区急需帐篷后,立刻到当地的一家帐篷厂采购,帐篷有两种规格,可供3人居住的小帐篷,价格每顶160元;可供10人居住的大帐篷,价格每顶400元.学校花去捐款96000元采购这两种帐篷,正好可供2300人居住. 学校准备租用甲、乙两种型号的卡车共20辆将所购帐篷紧急运往灾区,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷.
(1)求该校采购了多少顶3人小帐篷,多少顶10人住的大帐篷;
(2)学校应如何安排甲、乙两种型号的卡车可一次性将这批帐篷运往灾区?有几种方案?
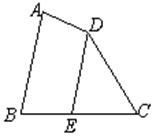
如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD︰∠E=1︰3,求∠E的度数.
如图,在平面直角坐标系中: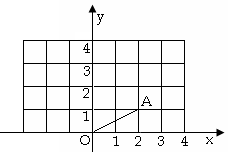
(1)写出点A的坐标;
(2)将线段OA向上平移两次,每次平移1个单位,再将线段向左平移2个单位,得到线段O′A′,写出点O、A的对应点O′、A′的坐标;
(3)在图中画出与线段OA相等的两条不同的线段.
为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2.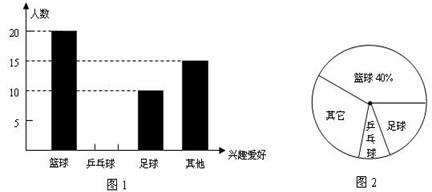
(1)该班共有多少名学生?若全年级共有1200名学生,估计全年级参加乒乓球活动的学生有多少名?
(2)请在图1中将“乒乓球”部分的图形补充完整,并求出扇形统计图中,表示“足球”的扇形圆心角的度数.
如图,四边形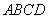 中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.