如图，一次函数y=kx+1（k≠0）与反比例函数y=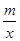
（m≠0）的图象有公共点A（1，2）．直线l⊥x轴于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C．
（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积？
计算： (1－
+
)(1－－)
已知a，b，c，d是四个不同的数，且a＞b，a+b=c+d，c+a＜d+b，求四个数中最大的数。
某品牌服装今年1月份售价是a元，3月份售价上涨10%，6月份又比3月份下降10%．
（1）用代数式分别表示3月份和6月份的售价；
（2）几月份去购买该品牌服装最便宜？为什么？
（1）用两根长度均为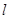
㎝的绳子，分别围成正方形和圆，如图所示，如果要使正方形的面积不大于25cm2，那么绳长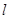应满足怎样的关系式.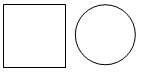
（2）如果要使圆的面积大于100cm2，那么绳长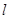应满足怎样的关系式？
（3）当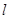=8㎝时，正方形和圆那个面积大？
用不等式表示下列关系.
（1）
与3的和的2倍不大于-5；
（2）
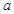除以2的商加上4至多为6；
（3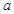）与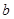
两数的平方和为非负数.