已知数列
的首项
,通项
(
为常数),且成等差数列。求:
(Ⅰ)
的值;
(Ⅱ) 数列
前
项和
的公式。
(本小题满分14分)
已知抛物线、椭圆、双曲线都经过点M(1,2),它们在x轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线方程;
(Ⅱ)若定点P(3,0),A为抛物线上任意一点,是否存在垂直于x轴的直线l被以AP为直径的圆截得的弦长为定值?若存在,求出l的方程;若不存在,说明理由。
(本小题满分13分)
已知函数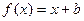 的图像与函数
的图像与函数 的图象相切,记
的图象相切,记
(Ⅰ)求实数b的值及函数F(x)的极值;
(Ⅱ)若关于x的方程F(x)=k恰有三个不等的实数根,求实数k的取值范围.
(本小题满分12分)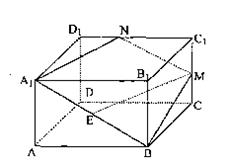
如图,在正四棱柱ABCD—A1B1C1D1中,AA1=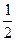 AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B—A1N—B1的正切值.
(本小题满分12分)
有一块边长为6m的正方形钢板,将其四个角各截去一个边长为x的小正方形,然后焊接成一个无盖的蓄水池。
(Ⅰ)写出以x为自变量的容积V的函数解析式V(x),并求函数V(x)的定义域;
(Ⅱ)指出函数V(x)的单调区间;
(Ⅲ)蓄水池的底边为多少时,蓄水池的容积最大?最大容积是多少?