如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)FC=AD;
(2)AB=BC+AD.
(本题10分)如图,已知E是平行四边形ABCD的BC边延长线上一点,AE交CD于F,CE= BC。
BC。
(1)求证:△ECF∽△ADF;
(2)S△ADF: S△CEF的值。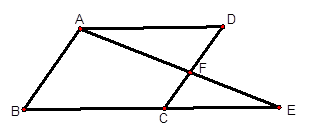
(本题10分)如图,在 中,
中, ,
, ,
, ,动点
,动点 从点
从点 开始沿边
开始沿边 向
向 以
以 的速度移动(不与点
的速度移动(不与点 重合),动点
重合),动点 从点
从点 开始沿边
开始沿边 向
向 以
以 的速度移动(不与点
的速度移动(不与点 重合).如果
重合).如果 、
、 分别从
分别从 、
、 同时出发,那么
同时出发,那么
(1)经过多少秒,四边形 的面积最小;(2)面积最小是多少?
的面积最小;(2)面积最小是多少?
(第25题图)
(本题10分)如图,已知A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC= OB.
OB.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若∠ACD=45°,OC=2,求弦AD的长。
(本题10分)为丰富学生的学习生活,某校九年级1班组织学生参加春游活动,所联系的旅行社收费标准如下:
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
(1)阅读下列材料并填空
例:解方程  +
+ =5
=5
解:① 当x<-3时,x+2<0 ,x+3<0,
所以 =-x-2,
=-x-2, =-x-3
=-x-3
所以原方程可化为 (1)=5
解得 x=(2)
② 当-3≤x <-2时 ,x+2<0 ,x+3≥0,
所以 =-x-2,
=-x-2, =x+3
=x+3
所以原方程可化为-x-2+x+3=5
1=5
所以此时原方程无解
③ 当x≥-2时 ,x+2≥0 ,x+3>0,
所以  = (3),
= (3), = (4)
= (4)
所以原方程可化为 (5)=5
解得 x=(6)
(2)用上面的解题方法解方程 -
- =x-6
=x-6