如图：抛物线y=－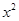
+bx+c与x轴交于A、B两点，与y轴交于点C，且∠BAC=α，∠ABC=
，tanα－tanβ=2，∠ACB=90°．
（1）求点C的坐标；
（2）求抛物线的解析式；
（3）若抛物线的顶点为P，求四边形ABPC的面积．
先化简，再求值：2(x＋1)(x-1)-3x(3＋x)＋(x＋5)(x-2)，其中x=-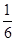
．
计算：（1）(am)2·am÷(-a2m)
（2）6x3-x(x2＋1)
（3）(a＋b)(a2-ab＋b2)
（4）(x-y)2-(x-2y) (x＋2y)
如图，在图a、图b、图c中都有直线m∥n，
（1）在图a中，∠2和∠1、∠3之间的数量关系是.
（2）猜想：在图b中，∠1、∠2、∠3、∠4之间的数量关系是。
（3）猜想：在图c中，∠2、∠4和∠1、∠3、∠5的数量关系式是 。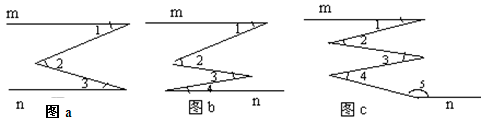
某天早晨，小王从家出发，骑摩托车前往工厂上班，途中在路旁一家饭店吃早餐，如图所示的是小王从家到工厂这一过程中行驶路程 s（千米）与时间t之间的关系．
（1）工厂离小王家多远？从家出发到工厂，小王共用了多少时间？
（2）小王吃早餐用了多少时间？
（3）小王吃早餐以前的速度快还是吃完早餐以后的速度快？最快时速达到多少？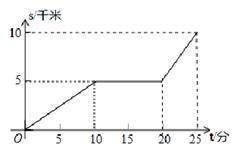
先化简，后求值：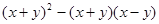
，其中
，
。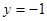