在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:

(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽甲所用的时间为 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡低?
如图,D是△ABC的BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=63°.求∠DAC的度数.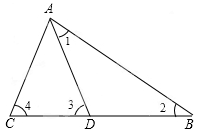
甲、乙两个车间工人人数不相等,若甲车间调10人到乙车间,则两车间人数相等;若乙车间调10人到甲车间,则甲车间的人数就是乙车间人数的2倍,求原来甲、乙两车间各有多少名工人?
某校七年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表: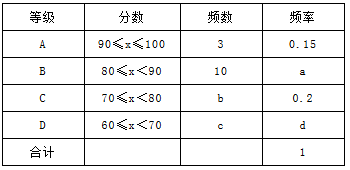
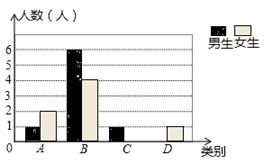
请你根据以上信息,解答下列问题:
(1)写出a,b,d的值并补全条形图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分.
如图所示,在所给的平面直角坐标系中,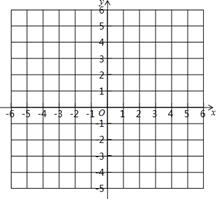
(1)描出下列各点,并将A、B、C三点顺次连接起来
A(2,3)、B(—2,—1)、C(3,2)
(2)将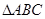 向左平移2个单位长度,向下平移1个单位长度,得到
向左平移2个单位长度,向下平移1个单位长度,得到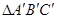 ,则点
,则点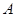 的对应点
的对应点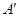 的坐标为 ;点
的坐标为 ;点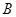 的对应点
的对应点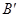 的坐标为 ;点
的坐标为 ;点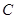 的对应点
的对应点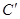 的坐标为
的坐标为
解下列不等式组,并把解集表示在数轴上
(1)
(2)