观察下列各式：
1×2＝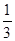
（1×2×3−0×1×2），
2×3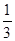＝（2×3×4−1×2×3），
3×4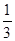＝（3×4×5−2×3×4），…
计算：3×（1×2+2×3+3×4+…+99×100）=（ ）
| A．97×98×99 | B．98×99×100 |
| C．99×100×101 | D．100×101×102 |
将分式
中的a、b都扩大到3倍,则分式的值 ( )
| A．不变 | B．扩大3倍 | C．扩大9倍 | D．扩大6倍 |
如图，在□ABCD中，∠ODA＝ 90°，AC＝10 cm，BD＝6 cm，则AD的长为 ( )
| A．4 cm | B．5 cm | C．6 cm | D．8 cm |
下列事件是随机事件的是（）
| A．购买一张福利彩票，中奖 |
| B．在一个标准大气压下，加热到100℃，水沸腾 |
| C．有一名运动员奔跑的速度是30米/秒 |
| D．在一个仅装着白球和黑球的袋中摸球，摸出红 |
已知O是口ABCD对角线的交点，△ABC的面积是3，则口ABCD的面积是（）
| A．3 | B．6 | C．9 | D．12 |
下列分式是最简分式的是（）
A． |
B． |
C． |
D． |