在数学的学习过程中，我们经常用以下的探索过程解决相关问题．
数学问题：三角形有3个顶点，如果在它的内部再画
个点，并以这
个点为顶点画三角形，那么可以剪得多少个这样的三角形？
探索规律：为了解决这个问题，我们可以从
、
、
等具体的、简单的情形入手，探索最多可以剪得的三角形个数的变化规律．
（1）填表：当三角形内有4个点时，把表格补充完整；
（2）你发现的变化规律是： ；
（3）猜想：当三角形内点的个数为时，最多可以剪得 个三角形；
像这样通过对简单情形的观察、分析，从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳．
问题解决：请你尝试用归纳的方法探索的
和是多少？
如图，某渔船在海面上朝正西方向以20海里/时匀速航行，在A处观测到灯塔C在北偏西60°方向上，航行1小时到达B处，此时观察到灯塔C在北偏西30°方向上，若该船继续向西航行至离灯塔距离最近的位置，求此时渔船到灯塔的距离（结果精确到1海里，参考数据：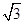
≈1．732）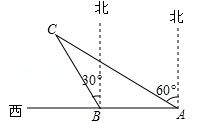
质地均匀的小正方体，六个面分别有数字“1”、“2”、“3”、“4”、“5”、“6”，同时投掷两枚，观察朝上一面的数字．
（1）求数字“1”出现的概率；
（2）求两个数字之和为偶数的概率．
如图，四边形ABCD、BEFG均为正方形，连接AG、CE．
（1）求证：AG=CE；
（2）求证：AG⊥CE．
先化简，再求值：
，其中
．
如图，己知抛物线y=k（x+1）（x-3k）（且k＞0）与x轴分别交于A、B两点，A点在B点左边，与Y轴交于C点，连接BC，过A点作AE∥CB交抛物线于E点，0为坐标原点．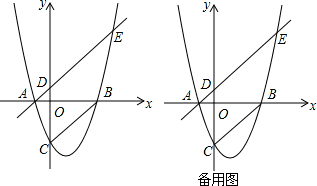
（1）用k表示点C的坐标（0，）；
（2）若k=1，连接BE，
①求出点E的坐标；
②在x轴上找点P，使以P、B、C为顶点的三角形与△ABE相似，求出P点坐标；
（3）若在直线AE上存在唯一的一点Q，连接OQ、BQ，使OQ⊥BQ，求k的值．