如图,直线 与x轴、y轴分别交于B、C两点,经过B、C两点的抛物线
与x轴、y轴分别交于B、C两点,经过B、C两点的抛物线 与x轴交于另一点A,线段BC与抛物线的对称轴l相交于点D,设抛物线的顶点为P,连接AD,线段AD与y轴相交于点E.
与x轴交于另一点A,线段BC与抛物线的对称轴l相交于点D,设抛物线的顶点为P,连接AD,线段AD与y轴相交于点E.
(1)求该抛物线的解析式及对称轴;
(2)连结AP,请在y轴正半轴上找一点Q,使Q、C、D为顶点的三角形与△ADP全等,并求出点Q的坐标.将∠CED绕点E顺时针旋转,边EC旋转后与线段BC相交于点M,边ED旋转后与对称轴l相交于点N,若2DM=DN,求点M的坐标.
解方程和不等式组:
(1) ;
;
(2) .
.
先化简,再求值: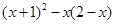 ,其中
,其中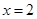 .
.
如图,在平面直角坐标系中,抛物线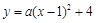 与
与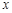 轴交于
轴交于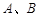 两点,与
两点,与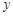 轴交于点
轴交于点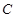 ,且点
,且点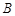 的坐标为
的坐标为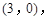 点
点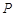 在这条抛物线上,且不与
在这条抛物线上,且不与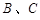 两点重合,过点
两点重合,过点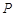 作
作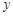 轴的垂线与射线
轴的垂线与射线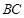 交于点
交于点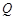 ,以
,以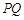 为边作
为边作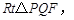 使
使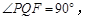 点
点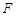 在点
在点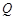 的下方,且
的下方,且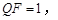 设线段
设线段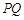 的长度为
的长度为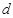 ,点
,点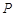 的横坐标为
的横坐标为 .
.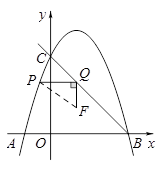
(1)求这条抛物线所对应的函数表达式;
(2)求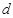 与
与 之间的函数关系式;
之间的函数关系式;
(3)当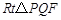 的边
的边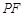 被
被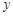 轴平分时,求
轴平分时,求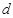 的值;
的值;
(4)以 为边作等腰直角三角形
为边作等腰直角三角形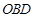 ,当
,当 时,直接写出点
时,直接写出点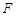 落在
落在 的边上时
的边上时 的值.
的值.
如图,在等边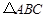 中,
中,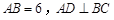 于点
于点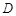 ,点
,点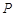 在边
在边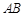 上运动,过点
上运动,过点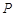 作
作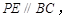 与边
与边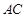 交于点
交于点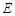 ,连结
,连结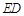 ,以
,以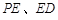 为邻边作□
为邻边作□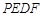 ,设□
,设□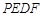 与
与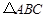 重叠部分图形的面积为
重叠部分图形的面积为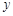 ,线段
,线段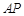 的长为
的长为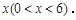
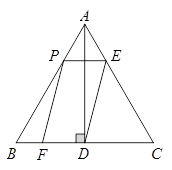
(1)求线段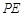 的长(用含
的长(用含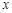 的代数式表示);
的代数式表示);
(2)当四边形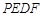 为菱形时,求
为菱形时,求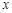 的值;
的值;
(3)求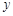 与
与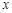 之间的函数关系式;
之间的函数关系式;
(4)设点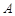 关于直线
关于直线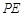 的对称点为点
的对称点为点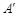 ,当线段
,当线段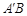 的垂直平分线与直线
的垂直平分线与直线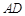 相交时,设其交点为
相交时,设其交点为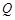 ,当点
,当点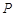 与点
与点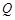 位于直线
位于直线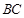 同侧(不包括点
同侧(不包括点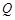 在直线
在直线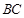 上)时,直接写出
上)时,直接写出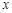 的取值范围.
的取值范围.
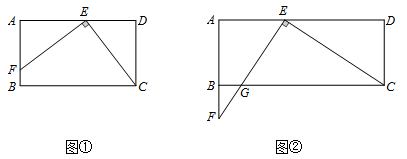
在矩形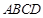 中,已知
中,已知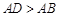 ,在边
,在边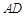 上取点
上取点 ,使
,使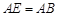 ,连结
,连结 ,过点
,过点 作
作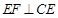 ,与边
,与边 或其延长线交于点
或其延长线交于点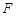 .
.
猜想:如图①,当点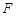 在边
在边 上时,线段
上时,线段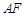 与
与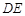 的大小关系为.
的大小关系为.
探究:如图②,当点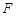 在边
在边 的延长线上时,
的延长线上时,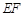 与边
与边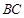 交于点
交于点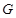 .判断线段
.判断线段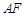 与
与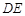 的大小关系,并加以证明.
的大小关系,并加以证明.
应用:如图②,若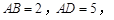 利用探究得到的结论,求线段
利用探究得到的结论,求线段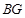 的长.
的长.